
【題目】設函數![]() 是偶函數.
是偶函數.
(1)若不等式![]() 對任意實數
對任意實數![]() 成立,求實數
成立,求實數![]() 的取值范圍;
的取值范圍;
(2)設函數![]() ,若
,若![]() 在
在![]() 上有零點,求實數
上有零點,求實數![]() 的取值范圍.
的取值范圍.
 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
【題目】為了解戶籍性別對生育二胎選擇傾向的影響,某地從育齡人群中隨機抽取了容量為![]() 的調查樣本,其中城鎮戶籍與農民戶籍各
的調查樣本,其中城鎮戶籍與農民戶籍各![]() 人;男性
人;男性![]() 人,女性
人,女性![]() 人.繪制不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數比例圖(如圖所示),其中陰影部分表示傾向選擇生育二胎的對應比例,則下列敘述中錯誤的是( )
人.繪制不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數比例圖(如圖所示),其中陰影部分表示傾向選擇生育二胎的對應比例,則下列敘述中錯誤的是( )
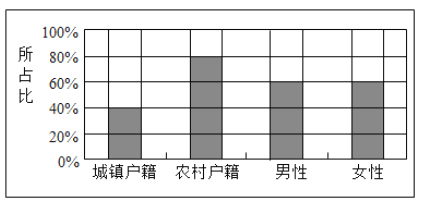
A.是否傾向選擇生育二胎與戶籍有關
B.是否傾向選擇生育二胎與性別無關
C.傾向選擇生育二胎的人員中,男性人數與女性人數相同
D.傾向選擇不生育二胎的人員中,農村戶籍人數少于城鎮戶籍人數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的個數是( )
①A=![]() 的子集有
的子集有![]() 個;
個;
②命題“![]() ”的否定是“
”的否定是“![]() 使得
使得![]() ”;
”;
③“![]() ”是“函數
”是“函數![]() 取得最大值”的充分不必要條件;
取得最大值”的充分不必要條件;
④根據對數定義,對數式![]() 化為指數式
化為指數式![]() ;
;
⑤若![]() ,則
,則![]() 的取值范圍為
的取值范圍為![]() ;
;
⑥![]() .
.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高三模擬考試的學生中隨機抽取60名學生,將其數學成績(均為整數)分成六組[90,100),[100,110),…,[140,150]后得到如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題:
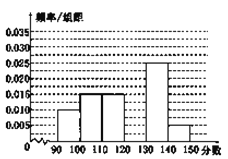
(1)求分數在[120,130)內的頻率;
(2)估計本次考試的中位數;
(3)用分層抽樣的方法在分數段為[110,130)的學生中抽取一個容量為6的樣本,將該樣本看成一個總體,從中任取2人,求至多有1人在分數段[120,130)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的上頂點為
的上頂點為![]() ,右焦點為
,右焦點為![]() ,直線
,直線![]() 與圓
與圓![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)若不過點![]() 的動直線
的動直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且
兩點,且![]() ,試探究:直線
,試探究:直線![]() 是否過定點,若是,求該定點的坐標,若不是,請說明.
是否過定點,若是,求該定點的坐標,若不是,請說明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 是定義在
是定義在![]() 上的奇函數,且當
上的奇函數,且當![]() 時,
時,![]() .
.
(Ⅰ)若![]() ,求函數
,求函數![]() 的解析式;
的解析式;
(Ⅱ)若![]() ,方程
,方程![]() 至少有兩個不等的解,求
至少有兩個不等的解,求![]() 的取值集合;
的取值集合;
(Ⅲ)若函數![]() 為
為![]() 上的單調減函數,
上的單調減函數,
①求![]() 的取值范圍;
的取值范圍;
②若不等式![]() 成立,求實數
成立,求實數![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 市實施全域旅游,將鄉村旅游公路建設與特色田園鄉村發展結合,精心打造全長365公里的“1號公路”,對內串聯區域內主要景區景點和自然村,對外通達周邊縣(市),以路引景、為景串線,形成一個“大環小圈、內連外引”的路網體系.如今的“1號公路”,不僅成為該市旅游業的“顏值擔當”,更成為推動鄉村振興的“實力擔當”,農村居住環境日益改善,新農村別墅隨處可見.圖①是一棟新農村別墅,它由上部屋頂和下部主體兩部分組成.如圖②,屋頂由四坡屋面構成,其中前后兩坡屋面
市實施全域旅游,將鄉村旅游公路建設與特色田園鄉村發展結合,精心打造全長365公里的“1號公路”,對內串聯區域內主要景區景點和自然村,對外通達周邊縣(市),以路引景、為景串線,形成一個“大環小圈、內連外引”的路網體系.如今的“1號公路”,不僅成為該市旅游業的“顏值擔當”,更成為推動鄉村振興的“實力擔當”,農村居住環境日益改善,新農村別墅隨處可見.圖①是一棟新農村別墅,它由上部屋頂和下部主體兩部分組成.如圖②,屋頂由四坡屋面構成,其中前后兩坡屋面![]() 和
和![]() 是全等的等腰梯形,左右兩坡屋面
是全等的等腰梯形,左右兩坡屋面![]() 和
和![]() 是全等的三角形.點
是全等的三角形.點![]() 在平面
在平面![]() 和
和![]() 上的射影分別為
上的射影分別為![]() (即:
(即:![]() 平面
平面![]() ,垂足為
,垂足為![]() ;
;![]() ,垂足為
,垂足為![]() ).已知
).已知![]() ,梯形
,梯形![]() 的面積是
的面積是![]() 面積的2.2倍.
面積的2.2倍.![]() .
.

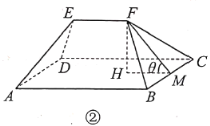
(1)當![]() 時,求屋頂面積的大小;
時,求屋頂面積的大小;
(2)求屋頂面積![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(3)已知上部屋頂造價與屋頂面積成正比,比例系數為![]() (
(![]() 為正的常數),下部主體造價與其高度成正比,比例系數為
為正的常數),下部主體造價與其高度成正比,比例系數為![]() .現欲造一棟上、下總高度為
.現欲造一棟上、下總高度為![]() 的別墅,試問:當
的別墅,試問:當![]() 為何值時,總造價最低?
為何值時,總造價最低?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com