【題目】已知四棱錐
中，
底面
，
，
，
，
.
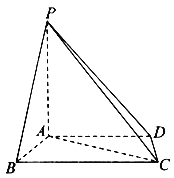
（1）當
變化時，點
到平面
的距離是否為定值？若是，請求出該定值；若不是，請說明理由；
（2）當直線
與平面所成的角為45°時，求二面角
的余弦值.
科目：高中數學 來源： 題型：
【題目】如圖，已知點
為拋物線
的焦點，過點
的直線交拋物線于
、
兩點，點
在拋物線上，使得
的重心
在
軸上，直線
交軸于點
，且在點的右側.記
、
的面積分別
、
.
（1）求
的值及拋物線的方程；
（2）求
的最小值及此時點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-4：極坐標與參數方程]
在直角坐標系
中，曲線
的參數方程為
（
是參數），以坐標原點
為極點，
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線的極坐標方程和曲線的直角坐標方程；
（2）若射線
與曲線交于，
兩點，與曲線交于，
兩點，求
取最大值時
的值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義：圓心到直線的距離與圓的半徑之比為直線關于圓的距離比
.
（1）設圓
求過
（2,0）的直線關于圓
的距離比
的直線方程；
（2）若圓
與
軸相切于點
（0,3）且直線
= 
關于圓
的距離比
，求此圓的
的方程；
（3）是否存在點
，使過
的任意兩條互相垂直的直線分別關于相應兩圓
的距離比始終相等？若存在，求出相應的點
點坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,四棱錐
中,
平面
,
, 
.
,
,
,
是
的中點.
(Ⅰ)證明:
⊥平面
;
(Ⅱ)若二面角
的余弦值是
,求
的值;
(Ⅲ)若
,在線段
上是否存在一點
,使得
⊥
. 若存在,確定點的位置;若不存在,說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著城市地鐵建設的持續推進，市民的出行也越來越便利．根據大數據統計，某條地鐵線路運行時，發車時間間隔t（單位：分鐘）滿足：4≤t≤15，
N，平均每趟地鐵的載客人數p(t)（單位：人）與發車時間間隔t近似地滿足下列函數關系：
，其中
.
(1）若平均每趟地鐵的載客人數不超過1500人，試求發車時間間隔t的值．
(2）若平均每趟地鐵每分鐘的凈收益為
（單位：元），問當發車時間間隔t為多少時，平均每趟地鐵每分鐘的凈收益最大？井求出最大凈收益．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
