
【題目】已知![]() ,若
,若![]() ,則
,則![]() 的最小值為__________;若
的最小值為__________;若![]() ,則
,則![]() 的最大值為__________.
的最大值為__________.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
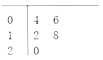
【題目】某縣共有90間農村淘寶服務站,隨機抽取5間,統計元旦期間的網購金額(單位:萬元)的莖葉圖如圖所示,其中莖為十位數,葉為個位數.若網購金額(單位:萬元)不小于18的服務站定義為優秀服務站,其余為非優秀服務站.從隨機抽取的5間服務站中再任取2間作網購商品的調查,則恰有1間是優秀服務站的概率為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為積極響應國家“陽光體育運動”的號召,某學校在了解到學生的實際運動情況后,發起以“走出教室,走到操場,走到陽光”為口號的課外活動倡議。為調查該校學生每周平均體育運動時間的情況,從高一高二基礎年級與高三三個年級學生中按照4:3:3的比例分層抽樣,收集300位學生每周平均體育運動時間的樣本數據(單位:小時),得到如圖所示的頻率分布直方圖。

(1)據圖估計該校學生每周平均體育運動時間.并估計高一年級每周平均體育運動時間不足4小時的人數;
(2)規定每周平均體育運動時間不少于6小時記為“優秀”,否則為“非優秀”,在樣本數據中,有30位高三學生的每周平均體育運動時間不少于6小時,請完成下列![]() 列聯表,并判斷是否有99%的把握認為“該校學生的每周平均體育運動時間是否“優秀”與年級有關”.
列聯表,并判斷是否有99%的把握認為“該校學生的每周平均體育運動時間是否“優秀”與年級有關”.
基礎年級 | 高三 | 合計 | |
優秀 | |||
非優秀 | |||
合計 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌經銷商在一廣場隨機采訪男性和女性用戶各50名,其中每天玩微信超過6小時的用戶列為“微信控”,否則稱其為“非微信控”,調查結果如下:
微信控 | 非微信控 | 合計 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合計 | 56 | 44 | 100 |
(1)根據以上數據,能否有95%的把握認為“微信控”與“性別”有關?
(2)現從調查的女性用戶中按分層抽樣的方法選出5人,求所抽取的5人中“微信控”和“非微信控”的人數;
(3)從(2)中抽取的5位女性中,再隨機抽取3人贈送禮品,試求抽取3人中恰有2人位“微信控”的概率.
參考公式: 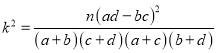 ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年12月份,我國湖北武漢出現了新型冠狀病毒,人感染后會出現發熱、咳嗽、氣促和呼吸困難等,嚴重的可導致肺炎甚至危及生命.為了增強居民防護意識,增加居民防護知識,某居委會利用網絡舉辦社區線上預防新冠肺炎知識答題比賽,所有居民都參與了防護知識網上答卷,最終甲、乙兩人得分最高進入決賽,該社區設計了一個決賽方案:①甲、乙兩人各自從![]() 個問題中隨機抽
個問題中隨機抽![]() 個.已知這
個.已知這![]() 個問題中,甲能正確回答其中的
個問題中,甲能正確回答其中的![]() 個,而乙能正確回答每個問題的概率均為
個,而乙能正確回答每個問題的概率均為![]() ,甲、乙兩人對每個問題的回答相互獨立、互不影響;②答對題目個數多的人獲勝,若兩人答對題目數相同,則由乙再從剩下的
,甲、乙兩人對每個問題的回答相互獨立、互不影響;②答對題目個數多的人獲勝,若兩人答對題目數相同,則由乙再從剩下的![]() 道題中選一道作答,答對則判乙勝,答錯則判甲勝.
道題中選一道作答,答對則判乙勝,答錯則判甲勝.
(1)求甲、乙兩人共答對![]() 個問題的概率;
個問題的概率;
(2)試判斷甲、乙誰更有可能獲勝?并說明理由;
(3)求乙答對題目數的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年1月10日,引發新冠肺炎疫情的COVID-9病毒基因序列公布后,科學家們便開始了病毒疫苗的研究過程.但是類似這種病毒疫苗的研制需要科學的流程,不是一朝一夕能完成的,其中有一步就是做動物試驗.已知一個科研團隊用小白鼠做接種試驗,檢測接種疫苗后是否出現抗體.試驗設計是:每天接種一次,3天為一個接種周期.已知小白鼠接種后當天出現抗體的概率為![]() ,假設每次接種后當天是否出現抗體與上次接種無關.
,假設每次接種后當天是否出現抗體與上次接種無關.
(1)求一個接種周期內出現抗體次數![]() 的分布列;
的分布列;
(2)已知每天接種一次花費100元,現有以下兩種試驗方案:
①若在一個接種周期內連續2次出現抗體即終止本周期試驗,進行下一接種周期,試驗持續三個接種周期,設此種試驗方式的花費為![]() 元;
元;
②若在一個接種周期內出現2次或3次抗體,該周期結束后終止試驗,已知試驗至多持續三個接種周期,設此種試驗方式的花費為![]() 元.
元.
比較隨機變量![]() 和
和![]() 的數學期望的大小.
的數學期望的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年春晚都是萬眾矚目的時刻,這些節目體現的文化內涵、歷史背景等反映了社會的進步.國家的富強,人民生活水平的提高等.某學校高三年級主任開學初為了解學生在看春晚后對節目體現的文化內涵、歷史背景等是否會在今年的高考題中體現進行過思考,特地隨機抽取100名高三學生(其中文科學生50,理科學生50名),進行了調查.統計數據如表所示(不完整):
“思考過” | “沒有思考過” | 總計 | |
文科學生 | 40 | 10 | |
理科學生 | 30 | ||
總計 | 100 |
(1)補充完整所給表格,并根據表格數據計算是否有![]() 的把握認為看春晚后會思考節目體現的文化內涵、歷史背景等與文理科學生有關;
的把握認為看春晚后會思考節目體現的文化內涵、歷史背景等與文理科學生有關;
(2)①現從上表的”思考過”的文理科學生中按分層抽樣選出7人.再從這7人中隨機抽取4人,記這4人中“文科學生”的人數為![]() ,試求
,試求![]() 的分布列與數學期望;
的分布列與數學期望;
②現設計一份試卷(題目知識點來自春晚相關知識整合與變化),假設“思考過”的學生及格率為![]() ,“沒有思考過”的學生的及格率為
,“沒有思考過”的學生的及格率為![]() .現從“思考過”與“沒有思考過”的學生中分別隨機抽取一名學生進行測試,求兩人至少有一個及格的概率.
.現從“思考過”與“沒有思考過”的學生中分別隨機抽取一名學生進行測試,求兩人至少有一個及格的概率.
附參考公式: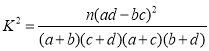 ,其中
,其中![]() .
.
參考數據:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某單位甲、乙、丙三個部門的員工人數分別為24,16,16.現采用分層抽樣的方法從中抽取7人,進行睡眠時間的調查.
(I)應從甲、乙、丙三個部門的員工中分別抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,現從這7人中隨機抽取3人做進一步的身體檢查.
(i)用X表示抽取的3人中睡眠不足的員工人數,求隨機變量X的分布列與數學期望;
(ii)設A為事件“抽取的3人中,既有睡眠充足的員工,也有睡眠不足的員工”,求事件A發生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com