
【題目】
已知![]() 在
在![]() 與
與![]() 時都取得極值.
時都取得極值.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() ,求
,求![]() 的單調區間和極值.
的單調區間和極值.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)f (x)的遞增區間為
;(Ⅱ)f (x)的遞增區間為![]() 和(1,+∞),遞減區間為
和(1,+∞),遞減區間為![]() .當x=-
.當x=-![]() 時,f(x)有極大值f
時,f(x)有極大值f![]() =
=![]() ;當x=1時,f(x)有極小值f(1)=-
;當x=1時,f(x)有極小值f(1)=-![]() .
.
【解析】
(1)因為函數在極值點處導數等于0,所以若f(x)在![]() 與
與![]() 時,都取得極值,則
時,都取得極值,則![]() 就可得到a,b的值;(2)先由
就可得到a,b的值;(2)先由![]() 求出函數中的c值,再求導數,令導數大于0,解得x的范圍是函數的增區間,令導數小于0,解得x的范圍是函數的減區間,增區間與減區間的分界點為極值點,且當極值點左側導數大于0,右側導數小于0時取得極大值,當極值點左側導數小于0,右側導數大于0時取得極小值,再把x的值代入原函數求出極大值與極小值
求出函數中的c值,再求導數,令導數大于0,解得x的范圍是函數的增區間,令導數小于0,解得x的范圍是函數的減區間,增區間與減區間的分界點為極值點,且當極值點左側導數大于0,右側導數小于0時取得極大值,當極值點左側導數小于0,右側導數大于0時取得極小值,再把x的值代入原函數求出極大值與極小值
試題解析:f′(x)=3x2+2ax+b=0.由題設知x=1,x=-![]() 為f′(x)=0的解.∴ -
為f′(x)=0的解.∴ -![]() a=1-
a=1-![]() ,
,![]() =1×
=1×![]() .∴ a=-
.∴ a=-![]() ,b=-2.經檢驗,這時x=1與x=-
,b=-2.經檢驗,這時x=1與x=-![]() 都是極值點.
都是極值點.
(2)f(x)=x3-![]() x2-2x+c,由f(-1)=-1-
x2-2x+c,由f(-1)=-1-![]() +2+c=
+2+c=![]() ,得c=1.∴ f (x)=x3-
,得c=1.∴ f (x)=x3-![]() x2-2x+1.
x2-2x+1.
x |
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| 遞增 | 極大值 | 遞減 | 極小值 | 遞增 |
∴ f (x)的遞增區間為![]() 和(1,+∞),遞減區間為
和(1,+∞),遞減區間為![]() .當x=-
.當x=-![]() 時,f(x)有極大值f
時,f(x)有極大值f![]() =
=![]() ;當x=1時,f(x)有極小值f(1)=-
;當x=1時,f(x)有極小值f(1)=-![]() .
.


科目:高中數學 來源: 題型:
【題目】
已知函數![]() .
.
(1)討論f(x)的單調性,并證明f(x)有且僅有兩個零點;
(2)設x0是f(x)的一個零點,證明曲線y=ln x 在點A(x0,ln x0)處的切線也是曲線![]() 的切線.
的切線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面幾種推理過程是演繹推理的是( )
A. 某校高三有8個班,1班有51人,2班有53人,3班有52人,由此推測各班人數都超過50人
B. 由三角形的性質,推測空間四面體的性質
C. 平行四邊形的對角線互相平分,菱形是平行四邊形,所以菱形的對角線互相平分
D. 在數列![]() 中,
中,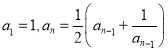 ,可得
,可得![]() ,由此歸納出
,由此歸納出![]() 的通項公式
的通項公式![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,點P到兩點(0,![]() ),(0,
),(0,![]() ),的距離之和等于4,設點P的軌跡為C.
),的距離之和等于4,設點P的軌跡為C.
(1)求C的方程.
(2)設直線![]() 與C交于A,B兩點,求弦長|AB|,并判斷OA與OB是否垂直,若垂直,請說明理由.
與C交于A,B兩點,求弦長|AB|,并判斷OA與OB是否垂直,若垂直,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是由矩形ADEB,Rt△ABC和菱形BFGC組成的一個平面圖形,其中AB=1,BE=BF=2,∠FBC=60°,將其沿AB,BC折起使得BE與BF重合,連結DG,如圖2.
(1)證明:圖2中的A,C,G,D四點共面,且平面ABC⊥平面BCGE;
(2)求圖2中的二面角BCGA的大小.

查看答案和解析>>
科目:高中數學 來源: 題型:
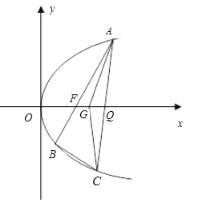
【題目】如圖,已知點![]() 為拋物線
為拋物線![]() ,點
,點![]() 為焦點,過點
為焦點,過點![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,點
兩點,點![]() 在拋物線上,使得
在拋物線上,使得![]() 的重心
的重心![]() 在
在![]() 軸上,直線
軸上,直線![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() 在點
在點![]() 右側.記
右側.記![]() 的面積為
的面積為![]() .
.
(1)求![]() 的值及拋物線的標準方程;
的值及拋物線的標準方程;
(2)求![]() 的最小值及此時點
的最小值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改革開放以來,人們的支付方式發生了巨大轉變.近年來,移動支付已成為主要支付方式之一.為了解某校學生上個月A,B兩種移動支付方式的使用情況,從全校所有的1000名學生中隨機抽取了100人,發現樣本中A,B兩種支付方式都不使用的有5人,樣本中僅使用A和僅使用B的學生的支付金額分布情況如下:
支付方式 | 不大于2000元 | 大于2000元 |
僅使用A | 27人 | 3人 |
僅使用B | 24人 | 1人 |
(Ⅰ)估計該校學生中上個月A,B兩種支付方式都使用的人數;
(Ⅱ)從樣本僅使用B的學生中隨機抽取1人,求該學生上個月支付金額大于2000元的概率;
(Ⅲ)已知上個月樣本學生的支付方式在本月沒有變化.現從樣本僅使用B的學生中隨機抽查1人,發現他本月的支付金額大于2000元.結合(Ⅱ)的結果,能否認為樣本僅使用B的學生中本月支付金額大于2000元的人數有變化?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓C:![]() 的焦點為F1(–1、0),
的焦點為F1(–1、0),
F2(1,0).過F2作x軸的垂線l,在x軸的上方,l與圓F2:![]() 交于點A,與橢圓C交于點D.連結AF1并延長交圓F2于點B,連結BF2交橢圓C于點E,連結DF1.已知DF1=
交于點A,與橢圓C交于點D.連結AF1并延長交圓F2于點B,連結BF2交橢圓C于點E,連結DF1.已知DF1=![]() .
.

(1)求橢圓C的標準方程;
(2)求點E的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓心在
中,已知圓心在![]() 軸上,半徑為2的圓
軸上,半徑為2的圓![]() 位于
位于![]() 軸右側,且與直線
軸右側,且與直線![]() 相切.
相切.
(1)求圓![]() 的方程;
的方程;
(2)在圓![]() 上,是否存在點
上,是否存在點![]() ,使得直線
,使得直線![]() 與圓
與圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,且
,且![]() 的面積最大?若存在,求出點
的面積最大?若存在,求出點![]() 的坐標及對應的
的坐標及對應的![]() 的面積;若不存在,請說明理由.
的面積;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com