
【題目】在平面直角坐標系xOy中,點P到兩點(0,![]() ),(0,
),(0,![]() ),的距離之和等于4,設點P的軌跡為C.
),的距離之和等于4,設點P的軌跡為C.
(1)求C的方程.
(2)設直線![]() 與C交于A,B兩點,求弦長|AB|,并判斷OA與OB是否垂直,若垂直,請說明理由.
與C交于A,B兩點,求弦長|AB|,并判斷OA與OB是否垂直,若垂直,請說明理由.
【答案】(1)x2![]() 1;(2)見解析
1;(2)見解析
【解析】
(1)由題意可知P點的軌跡為橢圓,并且得到c![]() ,a=2,求出b后可得橢圓的標準方程;
,a=2,求出b后可得橢圓的標準方程;
(2)設A(x1,![]() 1)B(x2,
1)B(x2,![]() 1),聯立方程
1),聯立方程 ,得17x2+4x﹣12=0,x1+x2
,得17x2+4x﹣12=0,x1+x2![]() ,x1x2
,x1x2![]() ,進而求解即可.
,進而求解即可.
(1)由條件知:P點的軌跡為焦點在y軸上的橢圓,其中c![]() ,a=2,∴b2=a2﹣c2=1,
,a=2,∴b2=a2﹣c2=1,
故軌跡C的方程為:x2![]() 1.
1.
(2)設A(x1,![]() 1)B(x2,
1)B(x2,![]() 1),聯立方程
1),聯立方程 ,得17x2+4x﹣12=0,x1+x2
,得17x2+4x﹣12=0,x1+x2![]() ,x1x2
,x1x2![]() ,
,
則|AB|

![]()
![]() (x1,
(x1,![]() 1),
1),![]() (x2,
(x2,![]() 1),
1),![]()
![]() x1x2+(
x1x2+(![]() 1)(
1)(![]() 1)
1)![]() x1x2
x1x2![]() (x1+x2)+1
(x1+x2)+1![]() (
(![]() )
)![]() (
(![]() )+1=0,
)+1=0,
即![]() ⊥
⊥![]() ,所以OA與OB垂直.
,所以OA與OB垂直.


科目:高中數學 來源: 題型:
【題目】對某校高一年級學生參加社區服務次數進行統計,隨機抽取M名學生作為樣本,得到這M名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
分組 | 頻數 | 頻率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合計 | M | 1 |

(1)求出表中M,p及圖中a的值;
(2)若該校高一學生有360人,試估計該校高一學生參加社區服務的次數在區間[15,20)內的人數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,請列舉出所有基本事件,并求至多1人參加社區服務次數在區間[20,25)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
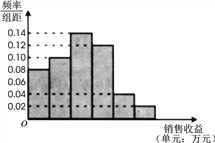
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入![]() 萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從
萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從![]() 開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
(1)根據頻率分布直方圖計算圖中各小長方形的寬度;
(2)試估計該公司投入![]() 萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
(3)該公司按照類似的研究方法,測得另外一些數據,并整理得到下表:
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 2 | 7 |
由表中的數據顯示, ![]() 與
與![]() 之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出
之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出![]() 關于
關于![]() 的回歸直線方程.
的回歸直線方程.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() ,圓
,圓![]() :
: ![]() 的圓心
的圓心![]() 在橢圓上,點
在橢圓上,點![]() 到橢圓
到橢圓![]() 的右焦點的距離為
的右焦點的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 作互相垂直的兩條直線
作互相垂直的兩條直線![]() ,且
,且![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,直線
兩點,直線![]() 交圓
交圓![]() 于
于![]() ,
, ![]() 兩點,且
兩點,且![]() 為
為![]() 的中點,求
的中點,求![]() 面積的取值范圍.
面積的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高三(2)班甲、乙兩名同學自高中以來每次考試成績的莖葉圖如圖,下列說法正確的是( )

A.乙同學比甲同學發揮的穩定,且平均成績也比甲同學高
B.乙同學比甲同學發揮的穩定,但平均成績不如甲同學高
C.甲同學比乙同學發揮的穩定,且平均成績也比乙同學高
D.甲同學比乙同學發揮的穩定,但平均成績不如乙同學高
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() ,為直線
,為直線![]() 上的動點,過
上的動點,過![]() 作
作![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() .
.
(1)證明:直線![]() 過定點:
過定點:
(2)若以![]() 為圓心的圓與直線
為圓心的圓與直線![]() 相切,且切點為線段
相切,且切點為線段![]() 的中點,求該圓的方程.
的中點,求該圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點A(0,1)且斜率為k的直線l與圓C:x2+y2﹣4x﹣6y+12=0相交于M、N兩點
(1)求實數k的取值范圍;
(2)求證:![]() 為定值;
為定值;
(3)若O為坐標原點,問是否存在直線l,使得![]() ,若存在,求直線l的方程,若不存在,說明理由.
,若存在,求直線l的方程,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為比較甲、乙兩地某月14時的氣溫情況,隨機選取該月中的5天,將這5天中14時的氣溫數據(單位:℃)制成如圖所示的莖葉圖,考慮以下結論:

①甲地該月14時的平均氣溫低于乙地該月14時的平均氣溫;
②甲地該月14時的平均氣溫高于乙地該月14時的平均氣溫;
③甲地該月14時的平均氣溫的標準差小于乙地該月14時的平均氣溫的標準差;
④甲地該月14時的平均氣溫的標準差大于乙地該月14時的平均氣溫的標準差,
其中根據莖葉圖能得到的統計結論的編號為( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com