
【題目】已知函數![]() .
.
(Ⅰ)過原點作曲線![]() 的切線,求切線方程;
的切線,求切線方程;
(Ⅱ)當![]() 時,討論曲線
時,討論曲線![]() 與曲線
與曲線![]() 公共點的個數.
公共點的個數.
【答案】(Ⅰ)![]() ;(Ⅱ)當
;(Ⅱ)當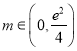 時,有0個公共點;當
時,有0個公共點;當![]() 時,有1個公共點;當
時,有1個公共點;當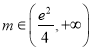 時,有2個公共點.
時,有2個公共點.
【解析】【試題分析】(1)依據題設借助導數的幾何意義分析求解;(2)先將零點的個數化為方程根的個數,再將方程問題轉化為函數的圖像問題,最后通過構造函數,運用導數的知識分析求解:
(Ⅰ)由題意,設切點為![]() ,由題意可得
,由題意可得
![]() ,即
,即![]() ,解得
,解得![]() ,即切點
,即切點![]() .
.
所以![]() ,所以切線方程為
,所以切線方程為![]() .
.
(Ⅱ)當![]() ,
, ![]() 時,曲線
時,曲線![]() 與曲線
與曲線![]() 的公共點個數
的公共點個數
即方程![]() 根的個數.
根的個數.
由![]() 得
得![]() .
.
令![]() ,則
,則![]() ,令
,令![]() ,解得
,解得![]() .
.
隨![]() 變化時,
變化時, ![]() ,
, ![]() 的變化情況如下表:
的變化情況如下表:
|
| 2 |
|
| — | 0 | + |
| ↘ | 極小值 | ↗ |
其中![]() .所以
.所以![]() 為
為![]() 在
在![]() 的最小值.
的最小值.
所以對曲線![]() 與曲線
與曲線![]() 公共點的個數,討論如下:
公共點的個數,討論如下:
當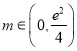 時,有0個公共點;當
時,有0個公共點;當![]() 時,有1個公共點;當
時,有1個公共點;當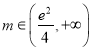 時,有2個公共點.
時,有2個公共點.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源: 題型:
【題目】甲、乙二人做射擊游戲,甲、乙射擊擊中與否是相互獨立事件.規則如下:若射擊一次擊中,則原射擊人繼續射擊;若射擊一次不中,就由對方接替射擊.已知甲、乙二人射擊一次擊中的概率均為![]() ,且第一次由甲開始射擊.①求前3次射擊中甲恰好擊中2次的概率____________;②求第4次由甲射擊的概率________.
,且第一次由甲開始射擊.①求前3次射擊中甲恰好擊中2次的概率____________;②求第4次由甲射擊的概率________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班同學利用寒假在三個小區進行了一次生活習慣是否符合低碳觀念的調查,若生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,這兩族人數占各自小區總人數的比例如下:
A小區 | 低碳族 | 非低碳族 |
比例 |
|
|
B小區 | 低碳族 | 非低碳族 |
比例 |
|
|
C小區 | 低碳族 | 非低碳族 |
比例 |
|
|
(1)從A,B,C三個社區中各選一人,求恰好有2人是低碳族的概率;
(2)在B小區中隨機選擇20戶,從中抽取的3戶中“非低碳族”數量為X,求X的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數, ![]() ).以原點
).以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,與直角坐標系
軸正半軸為極軸,與直角坐標系![]() 取相同的長度單位,建立極坐標系.設曲線
取相同的長度單位,建立極坐標系.設曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)設![]() 為曲線
為曲線![]() 上任意一點,求
上任意一點,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com