【題目】如圖，在三棱錐
中，
與
均為邊長是2的等邊三角形，平面
平面CBE，點O是BE的中點。
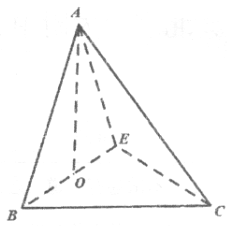
（1）求證：
；
（2）求直線AB與平面ACE所成角的正弦值。
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】提升城市道路通行能力，可為市民提供更多出行便利.我校某研究性學習小組對成都市一中心路段(限行速度為
千米/小時)的擁堵情況進行調查統計，通過數據分析發現：該路段的車流速度
(輛/千米)與車流密度
(千米/小時)之間存在如下關系:如果車流密度不超過
該路段暢通無阻(車流速度為限行速度)；當車流密度在
時，車流速度是車流密度的一次函數；車流密度一旦達到
該路段交通完全癱瘓(車流速度為零).
（1）求
關于的函數
（2）已知車流量(單位時間內通過的車輛數)等于車流密度與車流速度的乘積，求此路段車流量的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設等比數列
的公比為
，其前
項和為
，前項之積為
，并且滿足條件：
，
，
，下列結論中正確的是( )
A. 
B. 
C. 
是數列
中的最大值 D. 數列無最小值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種蔬菜從1月1日起開始上市，通過市場調查，得到該蔬菜種植成本
（單位：元/
）與上市時間
（單位：10天）的數據如下表：
時間 | 5 | 11 | 25 |
種植成本 | 15 | 10.8 | 15 |
（1）根據上表數據，從下列函數：
，
，
，
中（其中
），選取一個合適的函數模型描述該蔬菜種植成本與上市時間的變化關系；
（2）利用你選取的函數模型，求該蔬菜種植成本最低時的上市時間及最低種植成本.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業有甲、乙兩套設備生產同一種產品，為了檢測兩套設備的生產質量情況，隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本，檢測一項質量指標值，若該項質量指標值落在
內，則為合格品，否則為不合格品. 表1是甲套設備的樣本的頻數分布表，圖1是乙套設備的樣本的頻率分布直方圖.
表1：甲套設備的樣本的頻數分布表
質量指標值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數 | 1 | 4 | 19 | 20 | 5 | 1 |
圖1：乙套設備的樣本的頻率分布直方圖
（1）填寫下面列聯表，并根據列聯表判斷是否有90%的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關；
