
【題目】選修4-4:坐標系與參數方程
已知直線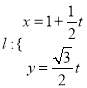 (
(![]() 為參數),曲線
為參數),曲線![]() (
(![]() 為參數).
為參數).
(1)設![]() 與
與![]() 相交于
相交于![]() 兩點,求
兩點,求![]() ;
;
(2)若把曲線![]() 上各點的橫坐標壓縮為原來的
上各點的橫坐標壓縮為原來的![]() 倍,縱坐標壓縮為原來的
倍,縱坐標壓縮為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,設點
,設點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離的最小值.
的距離的最小值.
【答案】(1)![]() 的普通方程為
的普通方程為![]() ,
, ![]() 的普通方程為
的普通方程為![]() ,(2)
,(2)![]()
【解析】試題分析:(1)將直線![]() 中的x與y代入到直線C1中,即可得到交點坐標,然后利用兩點間的距離公式即可求出|AB|.
中的x與y代入到直線C1中,即可得到交點坐標,然后利用兩點間的距離公式即可求出|AB|.
(2)將直線的參數方程化為普通方程,曲線C2任意點P的坐標,利用點到直線的距離公式P到直線的距離d,分子合并后利用兩角和與差的正弦函數公式及特殊角的三角函數值化為一個角的正弦函數,與分母約分化簡后,根據正弦函數的值域可得正弦函數的最小值,進而得到距離d的最小值即可.
試題解析:
解:(1)![]() 的普通方程為
的普通方程為![]() ,
, ![]() 的普通方程為
的普通方程為![]() ,
,
聯立方程組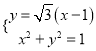 解得
解得![]() 與
與![]() 的交點為
的交點為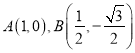 ,則
,則![]() ;
;
(2)![]() 的參數方程為
的參數方程為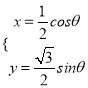 (
(![]() 為參數),故點
為參數),故點![]() 的坐標是
的坐標是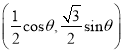 ,從而點
,從而點![]() 到直線
到直線![]() 的距離是
的距離是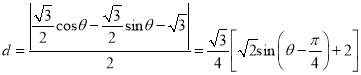 ,
,
由此當![]() 時,
時, ![]() 取得最小值,且最小值為
取得最小值,且最小值為![]() .
.


科目:高中數學 來源: 題型:
【題目】設f(x)是定義在R上的增函數,且對于任意的x都有f(1﹣x)+f(1+x)=0恒成立.如果實數m、n滿足不等式組![]() , 那么m2+n2的取值范圍是( )
, 那么m2+n2的取值范圍是( )
A.(3,7)
B.(9,25)
C.(13,49)
D.(9,49)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列函數f(x)與g(x)相等的一組是( )
A.f(x)=x﹣1,g(x)=![]() ﹣1
﹣1
B.f(x)=x2 , g(x)=(![]() )4
)4
C.f(x)=log2x2 , g(x)=2log2x
D.f(x)=tanx,g(x)=![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 的中點. 將
的中點. 將![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到幾何體
,得到幾何體![]() ,如圖2所示.
,如圖2所示.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與y軸的正半軸相交于點M,且橢圓E上相異兩點A、B滿足直線MA,MB的斜率之積為
與y軸的正半軸相交于點M,且橢圓E上相異兩點A、B滿足直線MA,MB的斜率之積為![]() .
.
(Ⅰ)證明直線AB恒過定點,并求定點的坐標;
(Ⅱ)求三角形ABM的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分13分)已知函數![]() (
(![]() 為常數,
為常數,![]() )
)
(1)若![]() 是函數
是函數![]() 的一個極值點,求
的一個極值點,求![]() 的值;
的值;
(2)求證:當![]() 時,
時,![]() 在
在![]() 上是增函數;
上是增函數;
(3)若對任意的![]() ,總存在
,總存在![]() ,使不等式
,使不等式![]() 成立,求正實數
成立,求正實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差大于零的等差數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,
,![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 是等差數列,且
是等差數列,且![]() ,求非零常數
,求非零常數![]() 的值.
的值.
(3)設![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和,是否存在正整數
項和,是否存在正整數![]() ,使得
,使得![]() 對任意的
對任意的![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com