
【題目】如圖,![]() 是南北方向的一條公路,
是南北方向的一條公路,![]() 是北偏東
是北偏東![]() 方向的一條公路,某風(fēng)景區(qū)的一段邊界為曲線
方向的一條公路,某風(fēng)景區(qū)的一段邊界為曲線![]() .為方便游客光,擬過曲線
.為方便游客光,擬過曲線![]() 上的某點分別修建與公路
上的某點分別修建與公路![]() ,
,![]() 垂直的兩條道路
垂直的兩條道路![]() ,
,![]() ,且
,且![]() ,
,![]() 的造價分別為5萬元
的造價分別為5萬元![]() 百米,40萬元
百米,40萬元![]() 百米,建立如圖所示的直角坐標(biāo)系
百米,建立如圖所示的直角坐標(biāo)系![]() ,則曲線符合函數(shù)
,則曲線符合函數(shù)![]() 模型,設(shè)
模型,設(shè)![]() ,修建兩條道路
,修建兩條道路![]() ,
,![]() 的總造價為
的總造價為![]() 萬元,題中所涉及的長度單位均為百米.
萬元,題中所涉及的長度單位均為百米.
(1)求![]() 解析式;
解析式;
(2)當(dāng)![]() 為多少時,總造價
為多少時,總造價![]() 最低?并求出最低造價.
最低?并求出最低造價.

【答案】(1)![]() ;(2)當(dāng)
;(2)當(dāng)![]() 時,總造價最低,最低造價為30萬元.
時,總造價最低,最低造價為30萬元.
【解析】
(1)求出![]() 的坐標(biāo),直線
的坐標(biāo),直線![]() 的方程,點
的方程,點![]() 到直線
到直線![]() 的距離,即可求
的距離,即可求![]() 解析式;
解析式;
(2)利用導(dǎo)數(shù)的方法最低造價.
解:(1)在如圖所示的直角坐標(biāo)系中,因為曲線![]() 的方程為
的方程為![]() ,
,
所以點![]() 坐標(biāo)為
坐標(biāo)為![]() ,
,
直線![]() 的方程為
的方程為![]() ,
,
則點![]() 到直線
到直線![]() 的距離為
的距離為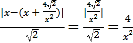 ,
,
又![]() 的造價為5萬元
的造價為5萬元![]() 百米,
百米,![]() 的造價為40萬元
的造價為40萬元![]() 百米.
百米.
則兩條道路總造價為![]() .
.
(2)因為![]() ,
,
所以![]() ,
,
令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
| 4 |
|
|
| 0 |
|
| 單調(diào)遞減 | 極小值 | 單調(diào)遞增 |
所以當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有最小值,最小值為
有最小值,最小值為![]() .
.
答:(1)兩條道路![]() ,
,![]() 總造價
總造價![]() 為
為![]() ;
;
(2)當(dāng)![]() 時,總造價最低,最低造價為30萬元.
時,總造價最低,最低造價為30萬元.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)若![]() ,函數(shù)
,函數(shù)![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,求
,求![]() 的值;
的值;
(2)當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 的最大值為
的最大值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從某校高中男生中隨機選取100名學(xué)生,將他們的體重(單位: ![]() )數(shù)據(jù)繪制成頻率分布直方圖,如圖所示.
)數(shù)據(jù)繪制成頻率分布直方圖,如圖所示.

(1)估計該校的100名同學(xué)的平均體重(同一組數(shù)據(jù)以該組區(qū)間的中點值作代表);
(2)若要從體重在![]() ,
, ![]() 內(nèi)的兩組男生中,用分層抽樣的方法選取5人,再從這5人中隨機抽取3人,記體重在
內(nèi)的兩組男生中,用分層抽樣的方法選取5人,再從這5人中隨機抽取3人,記體重在![]() 內(nèi)的人數(shù)為
內(nèi)的人數(shù)為![]() ,求其分布列和數(shù)學(xué)期望
,求其分布列和數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙二人參加某體育項目訓(xùn)練,近期的五次測試成績得分情況如圖所示.

(1)分別求出兩人得分的平均數(shù)與方差;
(2)根據(jù)圖和上面算得的結(jié)果,對兩人的訓(xùn)練成績作出評價.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() .
.
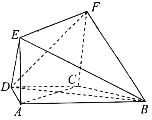
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)當(dāng)二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() ,求這個六面體
,求這個六面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,橢圓
,橢圓![]() 上一點
上一點![]() 與兩焦點構(gòu)成的三角形的周長為6,離心率為
與兩焦點構(gòu)成的三角形的周長為6,離心率為![]() ,
,

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,問在
兩點,問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為定值?證明你的結(jié)論.
為定值?證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司要了解某商品的年廣告費![]() (單位:萬元)對年銷售額
(單位:萬元)對年銷售額![]() (單位:萬元)的影響,對近4年的年廣告費
(單位:萬元)的影響,對近4年的年廣告費![]() 和年銷售額
和年銷售額![]() 數(shù)據(jù)作了初步調(diào)研,得到下面的表格:
數(shù)據(jù)作了初步調(diào)研,得到下面的表格:
年廣告費 | 2 | 3 | 4 | 5 |
年銷售額 | 26 | 39 | 49 | 54 |
用廣告費作解釋變量,年銷售額作預(yù)報變量,且![]() 適宜作為年銷售額
適宜作為年銷售額![]() 關(guān)于年廣告費
關(guān)于年廣告費![]() 的回歸方程類型.
的回歸方程類型.
(1)根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的回歸方程.
的回歸方程.
(2)已知商品的年利潤![]() 與
與![]() ,
,![]() 的關(guān)系式為
的關(guān)系式為![]() ,根據(jù)(1)中的結(jié)果,估計年廣告費
,根據(jù)(1)中的結(jié)果,估計年廣告費![]() 為何值時(小數(shù)點后保留兩位),年利潤的預(yù)報值最大?
為何值時(小數(shù)點后保留兩位),年利潤的預(yù)報值最大?
(對于數(shù)據(jù)![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
,![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
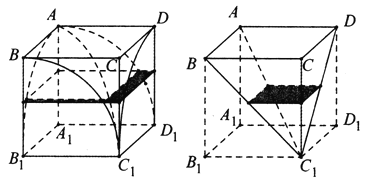
【題目】為推導(dǎo)球的體積公式,劉徽制造了一個牟合方蓋(在一個正方體內(nèi)作兩個互相垂直的內(nèi)切圓柱,這兩個圓柱的公共部分叫做牟合方蓋),但沒有得到牟合方蓋的體積.200年后,祖暅給出牟合方蓋的體積計算方法,其核心過程被后人稱為祖暅原理:緣冪勢既同,則積不容異.意思是,夾在兩個平行平面間的兩個幾何體被平行于這兩個平行平面的任意平面所截,如果截面的面積總相等,那么這兩個幾何體的體積也相等.現(xiàn)在截取牟合方蓋的八分之一,它的外切正方體![]() 的棱長為1,如圖所示,根據(jù)以上信息,則該牟合方蓋的體積為( )
的棱長為1,如圖所示,根據(jù)以上信息,則該牟合方蓋的體積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以下給出了4個命題:
(1)兩個長度相等的向量一定相等;
(2)相等的向量起點必相同;
(3)若![]() ,且
,且![]() ,則
,則![]() ;
;
(4)若向量![]() 的模小于
的模小于![]() 的模,則
的模,則![]() .
.
其中正確命題的個數(shù)共有( )
A.3 個B.2 個C.1 個D.0個
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com