
【題目】設△ABC中,角A,B,C所對的邊分別為a,b,c,則“∠C>90°”的一個充分非必要條件是( )
A.sin2A+sin2B<sin2C
B.sinA= ![]() ,(A為銳角),cosB=
,(A為銳角),cosB= ![]()
C.c2>2(a+b﹣1)
D.sinA<cosB
科目:高中數學 來源: 題型:
【題目】王先生家住 A 小區,他工作在 B 科技園區,從家開車到公司上班路上有 L1 , L2兩條路線(如圖),L1路線上有 A1 , A2 , A3三個路口,各路口遇到紅燈的概率均為 ![]() ;L2路線上有 B1 , B2兩個路.各路口遇到紅燈的概率依次為
;L2路線上有 B1 , B2兩個路.各路口遇到紅燈的概率依次為 ![]() ,
, ![]() .若走 L1路線,王先生最多遇到 1 次紅燈的概率為;若走 L2路線,王先生遇到紅燈次數 X 的數學期望為 .
.若走 L1路線,王先生最多遇到 1 次紅燈的概率為;若走 L2路線,王先生遇到紅燈次數 X 的數學期望為 . 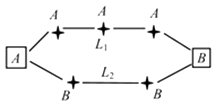
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在下列結論中: ①函數y=sin(kπ﹣x)(k∈Z)為奇函數;
②函數 ![]() 的圖象關于點
的圖象關于點 ![]() 對稱;
對稱;
③函數 ![]() 的圖象的一條對稱軸為
的圖象的一條對稱軸為 ![]() π;
π;
④若tan(π﹣x)=2,則cos2x= ![]() .
.
其中正確結論的序號為(把所有正確結論的序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.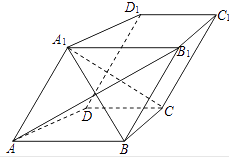
(1)求證:AB∥平面D1DCC1;
(2)求證:AB1⊥平面A1BC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別為A,B,C所對邊,a+b=4,(2﹣cosA)tan ![]() =sinA.
=sinA.
(1)求邊長c的值;
(2)若E為AB的中點,求線段EC的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線Ω:x2=2py(p>0),過點(0,2p)的直線與拋物線Ω交于A、B兩點,AB的中點為M,若點M到直線y=2x的最小距離為 ![]() ,則p=( )
,則p=( )
A.![]()
B.1
C.![]()
D.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(1+x)﹣ax, ![]() .
.
(Ⅰ)當b=1時,求g(x)的最大值;
(Ⅱ)若對x∈[0,+∞),f(x)≤0恒成立,求a的取值范圍;
(Ⅲ)證明 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系xOy中,橢圓C: ![]() 的離心率是
的離心率是 ![]() ,
,
拋物線E:x2=4y的焦點F是C的一個頂點.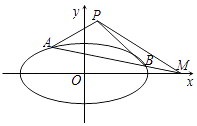
(1)求橢圓C的方程;
(2)設與坐標軸不重合的動直線l與C交于不同的兩點A和B,與x軸交于點M,且 ![]() 滿足kPA+kPB=2kPM , 試判斷點M是否為定點?若是定點求出點M的坐標;若不是定點請說明理由.
滿足kPA+kPB=2kPM , 試判斷點M是否為定點?若是定點求出點M的坐標;若不是定點請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com