
【題目】如圖,在四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.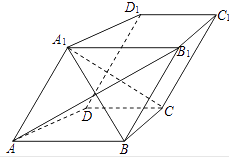
(1)求證:AB∥平面D1DCC1;
(2)求證:AB1⊥平面A1BC.
【答案】
(1)解:∵AB∥CD,CD平面D1DCC1,AB平面D1DCC1;
∴AB∥平面D1DCC1;
(2)解:在四棱柱ABCD﹣A1B1C1D1中,四邊形ABB1A1為平行四邊形,
∵AA1=AB,∴四邊形ABB1A1為菱形,∴AB1⊥A1B,
∵AB1⊥BC,A1B∩BC=B,
∴AB1⊥平面A1BC,
【解析】1、由線線平行得到線面平行。
2、根據題意可知四邊形ABB1A1為菱形,進而得到對角線互相垂直,再由已知根據線面垂直的判定定理可得證。
【考點精析】根據題目的已知條件,利用直線與平面平行的判定和直線與平面垂直的判定的相關知識可以得到問題的答案,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在(1+x+x2)n= ![]() x
x ![]() x2+…
x2+… ![]() xr+…
xr+… ![]() x2n﹣1
x2n﹣1 ![]() x2n的展開式中,把D
x2n的展開式中,把D ![]() ,D
,D ![]() ,D
,D ![]() …,D
…,D ![]() …,D
…,D ![]() 叫做三項式系數
叫做三項式系數
(1)求D ![]() 的值
的值
(2)根據二項式定理,將等式(1+x)2n=(1+x)n(x+1)n的兩邊分別展開可得,左右兩邊xn的系數相等,即C ![]() =(C
=(C ![]() )2+(C
)2+(C ![]() )2+(C
)2+(C ![]() )2+…+(C
)2+…+(C ![]() )2 , 利用上述思想方法,請計算D
)2 , 利用上述思想方法,請計算D ![]() C
C ![]() ﹣D
﹣D ![]() C
C ![]() +D
+D ![]() C
C ![]() ﹣…+(﹣1)rD
﹣…+(﹣1)rD ![]() C
C ![]() +..
+.. ![]() C
C ![]() C
C ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:①f(x)=sin(2x﹣ ![]() )的對稱軸為x=
)的對稱軸為x= ![]() ,k∈Z;②若函數y=2cos(ax﹣
,k∈Z;②若函數y=2cos(ax﹣ ![]() )(a>0)的最小正周期是π,則a=2;③函數f(x)=sinxcosx﹣1的最小值為﹣
)(a>0)的最小正周期是π,則a=2;③函數f(x)=sinxcosx﹣1的最小值為﹣ ![]() ;④函數y=sin(x+
;④函數y=sin(x+ ![]() )在[﹣
)在[﹣ ![]() ]上是增函數,其中正確命題的個數是( )
]上是增函數,其中正確命題的個數是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}是各項均為正數的等比數列,其前n項和為Sn , 若a1a5=64,S5﹣S3=48.
(1)求數列{an}的通項公式;
(2)對于正整數k,m,l(k<m<l),求證:“m=k+1且l=k+3”是“5ak , am , al這三項經適當排序后能構成等差數列”成立的充要條件;
(3)設數列{bn}滿足:對任意的正整數n,都有a1bn+a2bn﹣1+a3bn﹣2+…+anb1=32n+1﹣4n﹣6,且集合 ![]() 中有且僅有3個元素,試求λ的取值范圍.
中有且僅有3個元素,試求λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】閱讀如圖所示的程序框圖,則該算法的功能是( ) 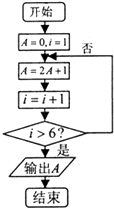
A.計算數列{2n﹣1}前5項的和
B.計算數列{2n﹣1}前5項的和
C.計算數列{2n﹣1}前6項的和
D.計算數列{2n﹣1}前6項的和
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC中,角A,B,C所對的邊分別為a,b,c,則“∠C>90°”的一個充分非必要條件是( )
A.sin2A+sin2B<sin2C
B.sinA= ![]() ,(A為銳角),cosB=
,(A為銳角),cosB= ![]()
C.c2>2(a+b﹣1)
D.sinA<cosB
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著霧霾日益嚴重,很多地區都實行了“限行”政策,現從某地區居民中,隨機抽取了300名居民了解他們對這一政策的態度,繪成如圖所示的2×2列聯表:
反對 | 支持 | 合計 | |
男性 | 70 | 60 | |
女性 | 50 | 120 | |
合計 |
(1)試問有沒有99%的把握認為對“限行”政策的態度與性別有關?
(2)用樣本估計總體,把頻率作為概率,若從該地區所有的居民(人數很多)中隨機抽取3人,用ξ表示所選3人中反對的人數,試寫出ξ的分布列,并求出ξ的數學期望.
K2= ![]() ,其中n=a+b+c+d獨立性檢驗臨界表:
,其中n=a+b+c+d獨立性檢驗臨界表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2lnx+x2﹣ax,a∈R.
(1)若函數y=f(x)在(0,+∞)上單調遞增,求實數a的取值范圍;
(2)若a=e,解不等式:f(x)<2;
(3)求證:當a>4時,函數y=f(x)只有一個零點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com