【題目】北京市2016年12個月的PM2.5平均濃度指數如圖所示．由圖判斷，四個季度中PM2.5的平均濃度指數方差最小的是（ ）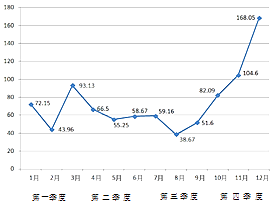 
A.第一季度
B.第二季度
C.第三季度
D.第四季度
第1卷單元月考期中期末系列答案科目：高中數學 來源： 題型：
【題目】已知雙曲線 
﹣ 
=1（a＞0，b＞0）的左、右焦點分別是F1 ， F2 ， 過F2的直線交雙曲線的右支于P，Q兩點，若|PF1|=|F1F2|，且3|PF2|=2|QF2|，則該雙曲線的離心率為（ ）
A.
B.
C.2
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在幾何體ABCDEF中，底面ABCD為矩形，EF∥CD，AD⊥FC．點M在棱FC上，平面ADM與棱FB交于點N．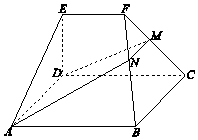 
（Ⅰ）求證：AD∥MN；
（Ⅱ）求證：平面ADMN⊥平面CDEF；
（Ⅲ）若CD⊥EA，EF=ED，CD=2EF，平面ADE∩平面BCF=l，求二面角A﹣l﹣B的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，底面ABCD為菱形，PC⊥平面ABCD，點E在棱PA上．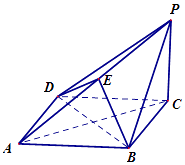 
（Ⅰ）求證：直線BD⊥平面PAC；
（Ⅱ）若PC∥平面BDE，求證：AE=EP；
（Ⅲ）是否存在點E，使得四面體A﹣BDE的體積等于四面體P﹣BDC的體積的 
？若存在，求出 
的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐S﹣ABCD中，底面ABCD是直角梯形，側棱SA丄底面ABCD，AB垂直于AD和BC，SA=AB=BC=2，AD=1．M是棱SB的中點．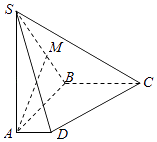
（1）求證：AM∥平面SCD；
（2）求平面SCD與平面SAB所成的二面角的余弦值；
（3）設點N是直線CD上的動點，MN與平面SAB所成的角為θ，求sinθ的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題p：函數f（x）=（m2﹣1） 
上為增函數；命題q：函數g（x）=x2﹣2elnx﹣m有零點．
（I）若p∨q為假命題，求實數m的取值范圍；
（Ⅱ）若p∨q為真命題，p∧q為假命題，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=sin（ωx﹣ 
）（ω＞0）的圖象與x軸的相鄰兩個交點的距離為 
．
（1）求w的值；
（2）設函數g（x）=f（x）+2cos2x﹣1，求g（x）在區間 
上的最大值和最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
