【題目】下面是某市環(huán)保局連續(xù)30天對空氣質(zhì)量指數(shù)的監(jiān)測數(shù)據(jù)：
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
（1）完成下面的頻率分布表；
（2）完成下面的頻率分布直方圖，并寫出頻率分布直方圖中
的值；
（3）在本月空氣質(zhì)量指數(shù)大于等于91的這些天中隨機選取兩天，求這兩天中至少有一天空氣質(zhì)量指數(shù)在區(qū)間
內(nèi)的概率．
分組 | 頻數(shù) | 頻率 |
[41，51) | 2 |
|
[51，61) | 3 |
|
[61，71) | 4 |
|
[71，81) | 6 |
|
[81，91) | ||
[91，101) | 3 | |
[101，111) |
|
【答案】（1）見解析；（2）見解析；（3）
【解析】
（1）根據(jù)已知條件中的數(shù)據(jù)，得到頻數(shù)，計算求得對應頻率，從而補全頻率分布表；（2）根據(jù)頻率分布表求得頻率分布直方圖缺失的矩形的高，從而補全圖形；再根據(jù)
的頻率計算得到矩形的高
；（3）列出所有基本事件，找到符合題意的基本事件個數(shù)，利用古典概型求出結果.
（1）需補全的數(shù)據(jù)如下圖所示：
分組 | 頻數(shù) | 頻率 |
|
|
|
|
|
|
|
|
|
（2）補全頻率分布直方圖，如下圖所示：
由已知，空氣質(zhì)量指數(shù)在區(qū)間的頻率為
（3）設
表示事件“在本月空氣質(zhì)量指數(shù)大于等于
的這些天中隨機選取兩天，這兩天中至少有一天空氣質(zhì)量指數(shù)在區(qū)間
內(nèi)”
由已知得：質(zhì)量指數(shù)在區(qū)間
內(nèi)的有
天，記這三天分別為
質(zhì)量指數(shù)在區(qū)間內(nèi)的有
天，記這兩天分別為
則選取的所有可能結果為：
，
，
，
，
，
，
，
，
，
，即基本事件數(shù)為
事件“至少有一天空氣質(zhì)量指數(shù)在區(qū)間內(nèi)”的可能結果為：
，，，，，，，，
基本事件數(shù)為
互動課堂系列答案
激活思維智能訓練課時導學練系列答案科目：高中數(shù)學 來源： 題型：
【題目】如圖,正四棱錐S-ABCD中,O為頂點在底面內(nèi)的投影,P為側棱SD的中點,且SO=OD,則直線BC與平面PAC的夾角是
A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某學校調(diào)查了20個班中有網(wǎng)上購物經(jīng)歷的人數(shù)，得到了如圖所示的莖葉圖，以
為分組，作出這組數(shù)的頻率分布直方圖，并說明頻率分布直方圖與莖葉圖之間的關系.
0 1 2 3 | 7 3 7 6 4 4 3 0 7 5 5 4 3 2 0 8 5 4 3 0 |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】[選修4-5：不等式選講]
已知函數(shù)
（
），若
的解集是
．
（1）求
的值；
（2）若關于
的不等式
有解，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下面幾種推理是類比推理的（ ）
A. 兩條直線平行，同旁內(nèi)角互補，如果
和
是兩條平行直線的同旁內(nèi)角，則
B. 由平面三角形的性質(zhì)，推測空間四邊形的性質(zhì)
C. 某校高二級有20個班，1班有51位團員，2班有53位團員，3班有52位團員，由此可以推測各班都超過50位團員.
D. 一切偶數(shù)都能被2整除，
是偶數(shù)，所以能被2整除.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某公司為了適應市場需求對產(chǎn)品結構做了重大調(diào)整，調(diào)整后初期利潤增長迅速，之后增長越來越慢，若要建立恰當?shù)暮瘮?shù)模型來反映該公司調(diào)整后利潤
與時間
的關系，可選用
A.一次函數(shù)B.二次函數(shù)
C.指數(shù)型函數(shù)D.對數(shù)型函數(shù)
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知圓
經(jīng)過橢圓
的右頂點
、下頂點
和上頂點
．
（1）求圓的標準方程；
（2）直線
經(jīng)過點
且與
垂直，
是直線上的動點，過點作圓的切線，切點分別為
，求四邊形
面積的最小值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】判斷下列函數(shù)的奇偶性：
（1）f(x)＝x＋1；
（2）f(x)＝x3＋3x，x∈[－4，4)；
（3）f(x)＝|x－2|－|x＋2|；
（4）f(x)＝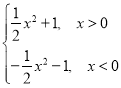
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
， 
．
（Ⅰ）當
時，求函數(shù)
的單調(diào)區(qū)間；
（Ⅱ）若曲線
在點
處的切線
與曲線
切于點
，求
的值；
（Ⅲ）若
恒成立，求
的最大值．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
