
【題目】如圖,某市有一條東西走向的公路![]() ,現(xiàn)欲經(jīng)過公路
,現(xiàn)欲經(jīng)過公路![]() 上的
上的![]() 處鋪設(shè)一條南北走向的公路
處鋪設(shè)一條南北走向的公路![]() .在施工過程中發(fā)現(xiàn)在
.在施工過程中發(fā)現(xiàn)在![]() 處的正北1百米的
處的正北1百米的![]() 處有一漢代古跡.為了保護古跡,該市決定以
處有一漢代古跡.為了保護古跡,該市決定以![]() 為圓心, 1百米為半徑設(shè)立一個圓形保護區(qū).為了連通公路
為圓心, 1百米為半徑設(shè)立一個圓形保護區(qū).為了連通公路![]() ,欲再新建一條公路
,欲再新建一條公路![]() ,點
,點 ![]() 分別在公路
分別在公路![]() 上,且求
上,且求![]() 與圓
與圓![]() 相切.
相切.
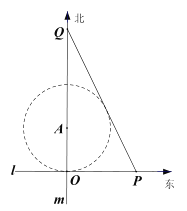
(1)當![]() 距
距![]() 處2百米時,求
處2百米時,求![]() 的長;
的長;
(2)當公路![]() 長最短時,求
長最短時,求![]() 的長.
的長.
【答案】(1)當![]() 距
距![]() 處2百米時,
處2百米時, ![]() 的長為
的長為![]() 百米;(2)當公路
百米;(2)當公路![]() 長最短時,
長最短時, ![]() 的長為
的長為![]() 百米.
百米.
【解析】試題分析:題目中涉及到直線與圓相切的條件,一般在平面直角坐標系中研究,所以先建立合適的坐標系;(1)已知點![]() ,則設(shè)直線
,則設(shè)直線![]() 的方程,可設(shè)截距(或點斜式),利用圓心到直線的距離等于半徑,求得
的方程,可設(shè)截距(或點斜式),利用圓心到直線的距離等于半徑,求得![]() 的坐標,從而得到
的坐標,從而得到![]() 的長;(2)研究
的長;(2)研究![]() 長的最小值,則需要建立目標函數(shù),選擇合適的變量,本小題依然可以設(shè)直線的兩個截距,則容易表示出的
長的最小值,則需要建立目標函數(shù),選擇合適的變量,本小題依然可以設(shè)直線的兩個截距,則容易表示出的![]() 長和直線方程,由相切再得到兩截距間的關(guān)系,消元后則得到一個一元的函數(shù),再利用導(dǎo)數(shù)研究它的最小值;
長和直線方程,由相切再得到兩截距間的關(guān)系,消元后則得到一個一元的函數(shù),再利用導(dǎo)數(shù)研究它的最小值;
試題解析:
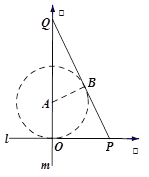
以![]() 為原點,直線
為原點,直線![]() 、
、![]() 分別為
分別為![]() 軸建立平面直角坐標系.
軸建立平面直角坐標系.
設(shè)![]() 與圓
與圓![]() 相切于點
相切于點![]() ,連結(jié)
,連結(jié)![]() ,以
,以![]() 百米為單位長度,則圓
百米為單位長度,則圓![]() 的方程為
的方程為![]() ,
,
(1)由題意可設(shè)直線![]() 的方程為
的方程為![]() ,即
,即![]() ,
, ![]() ,
,
∵![]() 與圓
與圓![]() 相切,∴
相切,∴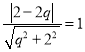 ,解得
,解得![]() ,
,
故當![]() 距
距![]() 處
處![]() 百米時,
百米時, ![]() 的長為
的長為![]() 百米.
百米.
(2)設(shè)直線![]() 的方程為
的方程為![]() ,即
,即![]() ,
, ![]() ,
,
∵![]() 與圓
與圓![]() 相切,∴
相切,∴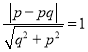 ,化簡得
,化簡得![]() ,則
,則![]() ,
,
令![]() ,∴
,∴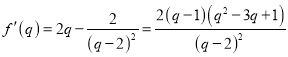
![]() ,
,
當![]() 時,
時, ![]() ,即
,即![]() 在
在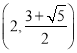 上單調(diào)遞減;
上單調(diào)遞減;
當![]() 時,
時, ![]() ,即
,即![]() 在
在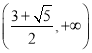 上單調(diào)遞增,
上單調(diào)遞增,
∴![]() 在
在![]() 時取得最小值,故當公路
時取得最小值,故當公路![]() 長最短時,
長最短時, ![]() 的長為
的長為![]() 百米.
百米.
答:(1)當![]() 距
距![]() 處
處![]() 百米時,
百米時, ![]() 的長為
的長為![]() 百米;(2)當公路
百米;(2)當公路![]() 長最短時,
長最短時, ![]() 的
的
長為![]() 百米.
百米.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,正方體ABCD-A1B1C1D1中,M、N、E、F分別是棱A1B1、A1D1、B1C1、C1D1的中點.
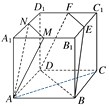
(1)求MN與AC所成角,并說明理由.
(2)求證:平面AMN∥平面EFDB.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】廣場舞是現(xiàn)代城市群眾文化、娛樂發(fā)展的產(chǎn)物,其兼具文化性和社會性,是精神文明建設(shè)成果的一個重要指標和象征.2015年某高校社會實踐小組對某小區(qū)跳廣場舞的人的年齡進行了凋查,隨機抽取了40名廣場舞者進行調(diào)查,將他們年齡分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如圖所示的頻率分布直方圖. 
(1)估計在40名廣場舞者中年齡分布在[40,70)的人數(shù);
(2)求40名廣場舞者年齡的中位數(shù)和平均數(shù)的估計值;
(3)若從年齡在[20,40)中的廣場舞者中任取2名,求這兩名廣場舞者年齡在[30,40)中的人數(shù)X的分布列及數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)![]() 滿足:在區(qū)間
滿足:在區(qū)間![]() 內(nèi)有且僅有一個實數(shù)
內(nèi)有且僅有一個實數(shù)![]() ,使得
,使得![]() 成立,則稱函數(shù)
成立,則稱函數(shù)![]() 具有性質(zhì)M.
具有性質(zhì)M.
![]() 判斷函數(shù)
判斷函數(shù)![]() 是否具有性質(zhì)M,說明理由;
是否具有性質(zhì)M,說明理由;
![]() 若函數(shù)
若函數(shù)![]() 具有性質(zhì)M,求實數(shù)a的取值范圍;
具有性質(zhì)M,求實數(shù)a的取值范圍;
![]() 若函數(shù)
若函數(shù)![]() 具有性質(zhì)M,求實數(shù)m的取值范圍.
具有性質(zhì)M,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某家庭進行理財投資,有兩種方式,甲為投資債券等穩(wěn)健型產(chǎn)品,乙為投資股票等風險型產(chǎn)品,設(shè)投資甲、乙兩種產(chǎn)品的年收益分別為![]() 、
、![]() 萬元,根據(jù)長期收益率市場預(yù)測,它們與投入資金
萬元,根據(jù)長期收益率市場預(yù)測,它們與投入資金![]() 萬元的關(guān)系分別為
萬元的關(guān)系分別為![]() ,
,![]() ,(其中
,(其中![]() ,
,![]() ,
,![]() 都為常數(shù)),函數(shù)
都為常數(shù)),函數(shù)![]() ,
,![]() 對應(yīng)的曲線
對應(yīng)的曲線![]() ,
,![]() 如圖所示.
如圖所示.
(1)求函數(shù)![]() 、
、![]() 的解析式;
的解析式;
(2)若該家庭現(xiàn)有![]() 萬元資金,全部用于理財投資,問:如何分配資金能使一年的投資獲得最大收益,其最大收益是多少萬元?
萬元資金,全部用于理財投資,問:如何分配資金能使一年的投資獲得最大收益,其最大收益是多少萬元?

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某程序框圖如圖所示,若輸出i的值為63,則判斷框內(nèi)可填入的條件是( ) 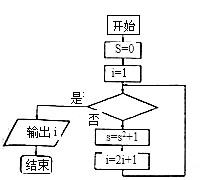
A.S>27
B.S≤27
C.S≥26
D.S<26
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() 且
且![]() 是定義域為R的奇函數(shù).
是定義域為R的奇函數(shù).
![]() 求k值;
求k值;
![]() 若
若![]() ,試判斷函數(shù)單調(diào)性并求使不等式
,試判斷函數(shù)單調(diào)性并求使不等式![]() 恒成立的t的取值范圍;
恒成立的t的取值范圍;
![]() 若
若![]() ,且
,且![]() 在
在![]() 上的最小值為
上的最小值為![]() ,求m的值.
,求m的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com