
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求證:過點
時,求證:過點![]() 有三條直線與曲線
有三條直線與曲線![]() 相切;
相切;
(Ⅱ)當![]() 時,
時, ![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(I)詳見解析;(II)![]() .
.
【解析】試題分析:
(1)首先對函數求導,寫出切線方程,討論方程根的分布可得過點![]() 有三條直線與曲線
有三條直線與曲線![]() 相切;
相切;
(2)利用題意構造函數![]() ,由新函數的性質可得實數
,由新函數的性質可得實數![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:解法一:(Ⅰ)當![]() 時,
時, ![]() ,
,
![]()
![]()
設直線與曲線![]() 相切,其切點為
相切,其切點為![]() ,
,
則曲線![]() 在點
在點![]() 處的切線方程為:
處的切線方程為: ![]() ,
,
因為切線過點![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
設![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
, ![]()
∴![]() 在三個區間
在三個區間![]() 上至少各有一個根
上至少各有一個根
又因為一元三次方程至多有三個根,所以方程![]() 恰有三個根,
恰有三個根,
故過點![]() 有三條直線與曲線
有三條直線與曲線![]() 相切.
相切.
(Ⅱ)∵當![]() 時,
時, ![]() ,即當
,即當![]() 時,
時, ![]()
∴當![]() 時,
時, ![]() ,
,
設![]() ,則
,則![]() ,
,
設![]() ,則
,則![]() .
.
(1)當![]() 時,∵
時,∵![]() ,∴
,∴![]() ,從而
,從而![]() (當且僅當
(當且僅當![]() 時,等號成立)
時,等號成立)
∴![]() 在
在![]() 上單調遞增,
上單調遞增,
又∵![]() ,∴當
,∴當![]() 時,
時, ![]() ,從而當
,從而當![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞減,又∵
上單調遞減,又∵![]() ,
,
從而當![]() 時,
時, ![]() ,即
,即![]()
于是當![]() 時,
時, ![]() .
.
(2)當![]() 時,令
時,令![]() ,得
,得![]() ,∴
,∴![]() ,
,
故當![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞減,
上單調遞減,
又∵![]() ,∴當
,∴當![]() 時,
時, ![]() ,
,
從而當![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞增,又∵
上單調遞增,又∵![]() ,
,
從而當![]() 時,
時, ![]() ,即
,即![]()
于是當![]() 時,
時, ![]() ,
,
綜合得![]() 的取值范圍為
的取值范圍為![]() .
.
解法二:(Ⅰ)當![]() 時,
時, ![]() ,
,
![]()
![]() ,
,
設直線與曲線![]() 相切,其切點為
相切,其切點為![]() ,
,
則曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,
,
因為切線過點![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]()
設![]() ,則
,則![]() ,令
,令![]() 得
得![]()
當![]() 變化時,
變化時, ![]() ,
, ![]() 變化情況如下表:
變化情況如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 極大值
| ↘ | 極小值 | ↗ |
∴![]() 恰有三個根,
恰有三個根,
故過點![]() 有三條直線與曲線
有三條直線與曲線![]() 相切.
相切.
(Ⅱ)同解法一.


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:高中數學 來源: 題型:
【題目】
如圖,⊙O內切于△ABC的邊于D,E,F,AB=AC,連接AD交⊙O于點H,直線HF交BC的延長線于點G.
(Ⅰ)求證:圓心O在直線AD上;
(Ⅱ)求證:點C是線段GD的中點.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為落實《課標》所倡導的課程理念,切實提高學生的綜合素質,某校高二年級開設“趣味數學”、“趣味物理”、“趣味化學”3門任意選修課程,供年級300位文科生自由選擇2門(不可多選或少選),選課情況如下表:

(Ⅰ)為了解學生選課情況,現采用分層抽樣方法抽取了三科作業共50本,統計發現“趣味物理”有18本,試根據這一數據估計![]() ,
, ![]() 的值;
的值;
(Ⅱ)為方便開課,學校要求![]() ,
, ![]() ,計算
,計算![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,點D是AB的中點. 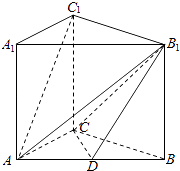
(1)求證:AC1∥平面CDB1
(2)求證:AC⊥BC1
(3)求直線AB1與平面BB1C1C所成的角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,函數
,函數![]() ,且
,且![]() 圖象上一個最高點為
圖象上一個最高點為![]() 與
與![]() 最近的一個最低點的坐標為
最近的一個最低點的坐標為![]() .
.
(Ⅰ)求函數![]() 的解析式;
的解析式;
(Ⅱ)設![]() 為常數,判斷方程
為常數,判斷方程![]() 在區間
在區間![]() 上的解的個數;
上的解的個數;
(Ⅲ)在銳角![]() 中,若
中,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x|,g(x)=lg(ax2﹣4x+1),若對任意x1∈R,都存在在x2∈R,使f(x1)=g(x2),則實數a的取值范圍是( )
A.(﹣∞,4]
B.(0,4]
C.(﹣4,0]
D.[0,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數 ![]() ,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 設c1≥c2≥c3 , 則c1﹣c3=( )
,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 設c1≥c2≥c3 , 則c1﹣c3=( )
A.6
B.8
C.2
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017衡陽第二次聯考】已知四棱錐![]() 中,底面為矩形,
中,底面為矩形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 上一點,
上一點, ![]() 為
為![]() 的中點.
的中點.
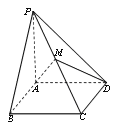
(1)在圖中作出平面![]() 與
與![]() 的交點
的交點![]() ,并指出點
,并指出點![]() 所在位置(不要求給出理由);
所在位置(不要求給出理由);
(2)求平面![]() 將四棱錐
將四棱錐![]() 分成上下兩部分的體積比.
分成上下兩部分的體積比.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com