
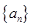 的首項為
的首項為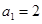 ,公比為
,公比為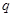 (
(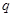 為正整數),且滿足
為正整數),且滿足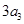 是
是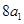 與
與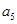 的等差中項;數列
的等差中項;數列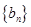 滿足
滿足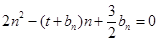 (
(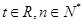 ).
).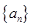 的通項公式;
的通項公式;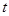 的值,使得數列
的值,使得數列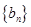 為等差數列;
為等差數列;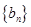 為等差數列時,對每個正整數
為等差數列時,對每個正整數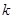 ,在
,在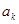 與
與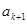 之間插入
之間插入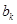 個2,得到一個新數列
個2,得到一個新數列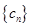 . 設
. 設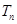 是數列
是數列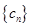 的前
的前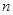 項和,試求滿足
項和,試求滿足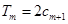 的所有正整數
的所有正整數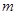 .
.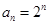 ;(Ⅱ)
;(Ⅱ)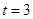 ;(Ⅲ)
;(Ⅲ)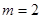
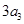 是
是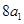 與
與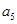 的等比中項可得
的等比中項可得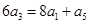 ,根據等比數列基本量可得到關于
,根據等比數列基本量可得到關于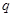 的方程,從而求出
的方程,從而求出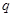 ,由
,由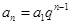 得到數列
得到數列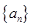 的通項公式; (Ⅱ)由題中所給
的通項公式; (Ⅱ)由題中所給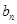 關于
關于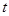 表達式
表達式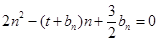 化簡得用
化簡得用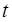 表示
表示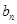 的表達式,即
的表達式,即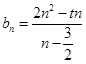 ,這樣可聯想到去求出
,這樣可聯想到去求出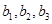 ,利用等差中項可求出
,利用等差中項可求出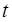 的值,并由此求出
的值,并由此求出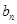 的表達式,最后根據求
的表達式,最后根據求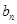 的表達式結合等差數列的定義去證明它是一個等差數列; (Ⅲ)由(Ⅰ)知數列
的表達式結合等差數列的定義去證明它是一個等差數列; (Ⅲ)由(Ⅰ)知數列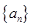 的通項公式,由(Ⅱ)知數列
的通項公式,由(Ⅱ)知數列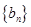 的通項公式,結合題中要求分析得:
的通項公式,結合題中要求分析得: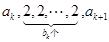 ,
, 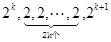 ,則可得出數列
,則可得出數列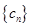 的大體如下:
的大體如下: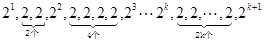 ,可見數列
,可見數列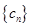 的前三項均為
的前三項均為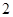 ,由此可驗證
,由此可驗證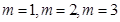 的具體情況,可得其中
的具體情況,可得其中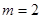 符合題中要求,當
符合題中要求,當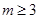 時,分析
時,分析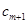 不可能為
不可能為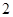 ,因為前面的永大于
,因為前面的永大于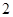 ,那么要存在
,那么要存在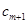 肯定為
肯定為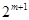 ,這樣就可得到關于
,這樣就可得到關于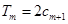 一個假設的等式,并可化簡得關于
一個假設的等式,并可化簡得關于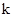 的表達式
的表達式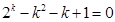 ,根據特點可設出對應的函數
,根據特點可設出對應的函數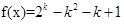 ,最后由導數在函數中的運用去判斷出在
,最后由導數在函數中的運用去判斷出在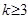 上函數恒為正.
上函數恒為正.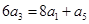 ,所以
,所以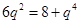 ,
,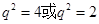 (舍),則
(舍),則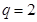 3分
3分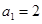 ,所以
,所以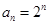 5分
5分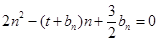 ,得
,得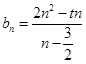 ,
,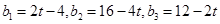 ,
,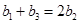 ,得
,得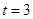 8分
8分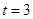 時,
時,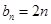 ,由
,由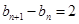 (常數)知此時數列
(常數)知此時數列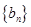 為等差數列 10分
為等差數列 10分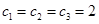 ,易知
,易知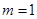 不合題意,
不合題意,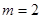 適合題意 11分
適合題意 11分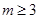 時,若后添入的數2
時,若后添入的數2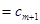 ,則一定不適合題意,從而
,則一定不適合題意,從而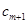 必是數列
必是數列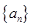 中的
中的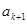 ,則
,則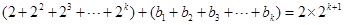 ,
,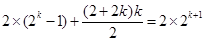 ,即
,即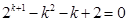 13分
13分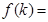
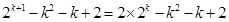 ,則
,則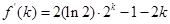 ,
,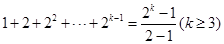 ,
,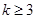 時,
時,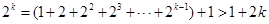 ,又
,又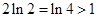 ,
,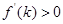 ,故
,故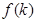 在[3,
在[3,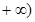 遞增.
遞增.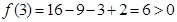 知
知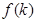 =0在[3,
=0在[3,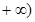 無解,
無解,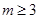 都不合題意 15分
都不合題意 15分

 中考解讀考點精練系列答案
中考解讀考點精練系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com