
【題目】某互聯網公司為了確定下一季度的前期廣告投入計劃,收集了近期前期廣告投入量![]() (單位:萬元)和收益
(單位:萬元)和收益![]() (單位:萬元)的數據。對這些數據作了初步處理,得到了下面的散點圖(共
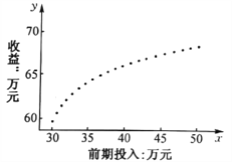
(單位:萬元)的數據。對這些數據作了初步處理,得到了下面的散點圖(共![]() 個數據點)及一些統計量的值.為了進一步了解廣告投入量
個數據點)及一些統計量的值.為了進一步了解廣告投入量![]() 對收益
對收益![]() 的影響,公司三位員工①②③對歷史數據進行分析,查閱大量資料,分別提出了三個回歸方程模型:
的影響,公司三位員工①②③對歷史數據進行分析,查閱大量資料,分別提出了三個回歸方程模型:
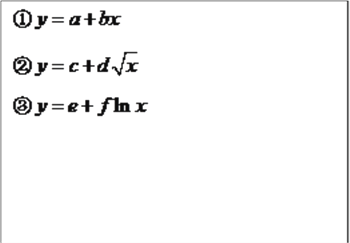
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根據![]() ,
, ![]() ,參考數據:
,參考數據: ![]() ,
, ![]() .
.
(1)根據散點圖判斷,哪一位員工提出的模型不適合用來描述![]() 與
與![]() 之間的關系?簡要說明理由.
之間的關系?簡要說明理由.
(2)根據(1)的判斷結果及表中數據,在余下兩個模型中分別建立收益![]() 關于投入量
關于投入量![]() 的關系,并從數據相關性的角度考慮,在余下兩位員工提出的回歸模型中,哪一個是最優模型(即更適宜作為收益
的關系,并從數據相關性的角度考慮,在余下兩位員工提出的回歸模型中,哪一個是最優模型(即更適宜作為收益![]() 的回歸方程)?說明理由;
的回歸方程)?說明理由;
附:對于一組數據![]() ,
, ![]() ,…,
,…, ![]() ,其回歸直線
,其回歸直線![]() 的斜率、截距的最小二乘估計以及相關系數分別為:
的斜率、截距的最小二乘估計以及相關系數分別為:
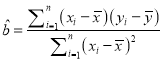 ,
, ![]() ,
, 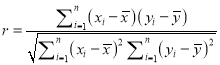 ,
,
其中![]() 越接近于
越接近于![]() ,說明變量
,說明變量![]() 與
與![]() 的線性相關程度越好.
的線性相關程度越好.
 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】
如圖,在直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,底面ABCD為等腰梯形,AB//CD,AB=4,BC=CD=2,AA
中,底面ABCD為等腰梯形,AB//CD,AB=4,BC=CD=2,AA![]() =2,E、E
=2,E、E![]() 分別是棱AD、AA
分別是棱AD、AA![]() 的中點.
的中點.

(1)設F是棱AB的中點,證明:直線EE![]() //平面FCC
//平面FCC![]() ;
;
(2)證明:平面D1AC⊥平面BB1C1C.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABCDEF中,ABCD是正方形,BF⊥平面ABCD,DE⊥平面ABCD,BF=DE,點M為棱AE的中點.
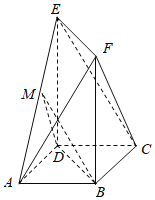
(1)求證:平面BMD∥平面EFC;
(2)若AB=1,BF=2,求三棱錐A-CEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在某商業區周邊有 兩條公路![]() 和
和![]() ,在點
,在點![]() 處交匯,該商業區為圓心角
處交匯,該商業區為圓心角![]() ,半徑3
,半徑3![]() 的扇形,現規劃在該商業區外修建一條公路
的扇形,現規劃在該商業區外修建一條公路![]() ,與
,與![]() ,
,![]() 分別交于
分別交于![]() ,要求
,要求![]() 與扇形弧相切,切點
與扇形弧相切,切點![]() 不在
不在![]() ,
,![]() 上.
上.
(1)設![]() 試用
試用![]() 表示新建公路
表示新建公路![]() 的長度,求出
的長度,求出![]() 滿足的關系式,并寫出
滿足的關系式,并寫出![]() 的范圍;
的范圍;
(2)設![]() ,試用
,試用![]() 表示新建公路
表示新建公路![]() 的長度,并且確定
的長度,并且確定![]() 的位置,使得新建公路
的位置,使得新建公路![]() 的長度最短.
的長度最短.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數y=f(x)對定義域內的每一個值x1,在其定義域內都存在唯一的x2,使f(x1)f(x2)=1成立,則稱該函數為“依賴函數”.
(1) 判斷函數g(x)=2x是否為“依賴函數”,并說明理由;
(2) 若函數f(x)=(x–1)2在定義域[m,n](m>1)上為“依賴函數”,求實數m、n乘積mn的取值范圍;
(3) 已知函數f(x)=(x–a)2 (a<![]() )在定義域[
)在定義域[![]() ,4]上為“依賴函數”.若存在實數x[
,4]上為“依賴函數”.若存在實數x[![]() ,4],使得對任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求實數s的最大值.
,4],使得對任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求實數s的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() ,
,![]() 為坐標原點,
為坐標原點,![]() 為橢圓
為橢圓![]() 的左焦點,離心率為
的左焦點,離心率為![]() ,直線
,直線![]() 與橢圓相交于
與橢圓相交于![]() ,
,![]() 兩點.
兩點.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 是弦
是弦![]() 的中點,
的中點,![]() 是橢圓
是橢圓![]() 上一點,求
上一點,求![]() 的面積最大值.
的面積最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人同時從A地趕往B地,甲先騎自行車到中點改為跑步,而乙則是先跑步,到中點后改為騎自行車,最后兩人同時到達B地.已知甲騎自行車比乙騎自行車快.若每人離開甲地的距離![]() 與所用時間
與所用時間![]() 的函數用圖象表示,則甲、乙對應的圖象分別是
的函數用圖象表示,則甲、乙對應的圖象分別是
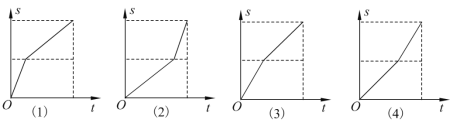
A.甲是(1),乙是(2)B.甲是(1),乙是(4)
C.甲是(3),乙是(2)D.甲是(3),乙是(4)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com