
【題目】若函數y=f(x)對定義域內的每一個值x1,在其定義域內都存在唯一的x2,使f(x1)f(x2)=1成立,則稱該函數為“依賴函數”.
(1) 判斷函數g(x)=2x是否為“依賴函數”,并說明理由;
(2) 若函數f(x)=(x–1)2在定義域[m,n](m>1)上為“依賴函數”,求實數m、n乘積mn的取值范圍;
(3) 已知函數f(x)=(x–a)2 (a<![]() )在定義域[
)在定義域[![]() ,4]上為“依賴函數”.若存在實數x[
,4]上為“依賴函數”.若存在實數x[![]() ,4],使得對任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求實數s的最大值.
,4],使得對任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求實數s的最大值.
【答案】(1)g(x)=2x是“依賴函數”(2)![]() (3)
(3)![]()
【解析】試題分析:(1)取![]() ,可驗證函數為依賴函數;(2)化簡條件得
,可驗證函數為依賴函數;(2)化簡條件得![]() ,從而
,從而![]() ,利用單調性求值域即可;(3)由題意知存在
,利用單調性求值域即可;(3)由題意知存在![]() ,使得對任意的t∈R,有不等式
,使得對任意的t∈R,有不等式![]() 都成立,即
都成立,即![]() 恒成立,分離參數可得
恒成立,分離參數可得![]() ,轉化為求最值問題處理.
,轉化為求最值問題處理.
試題解析:
(1) 對于函數g(x)=2x的定義域R內任意的x1,取x2= –x1,則g(x1)g(x2)=1,
且由g(x)=2x在R上單調遞增,可知x2的取值唯一,
故g(x)=2x是“依賴函數”;
(2) 因為m>1,f(x)=(x–1)2在[m,n]遞增,故f(m)f(n)=1,即(m–1)2(n–1)2=1,
由n>m>1,得(m–1) (n–1) =1,故![]() ,
,
由n>m>1,得1<m<2,
從而![]() 在
在![]() 上單調遞減,故
上單調遞減,故![]() ,
,
(3) 因![]() ,故
,故![]() 在
在![]() 上單調遞增,
上單調遞增,
從而![]() ,即
,即![]() ,進而
,進而![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
從而,存在![]() ,使得對任意的t∈R,有不等式
,使得對任意的t∈R,有不等式![]() 都成立,即
都成立,即![]() 恒成立,由
恒成立,由![]() ,
,
得![]() ,由
,由![]() ,可得
,可得![]() ,
,
又![]() 在
在![]() 單調遞增,故當
單調遞增,故當![]() 時,
時, ![]() ,
,
從而![]() ,解得
,解得![]() ,故實數
,故實數![]() 的最大值為
的最大值為![]() .
.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且橢圓
,且橢圓![]() 過點
過點 .過點
.過點![]() 做兩條相互垂直的直線
做兩條相互垂直的直線![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四點.
四點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若![]() ,
, ![]() ,探究:直線
,探究:直線![]() 是否過定點?若是,請求出定點坐標;若不是,請說明理由.
是否過定點?若是,請求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天水市第一次聯考后,某校對甲、乙兩個文科班的數學考試成績進行分析,
規定:大于或等于120分為優秀,120分以下為非優秀.統計成績后,
得到如下的![]() 列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為
列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為![]() .
.
優秀 | 非優秀 | 合計 | |
甲班 | 10 | ||
乙班 | 30 | ||
合計 | 110 |
(1)請完成上面的列聯表;
(2)根據列聯表的數據,若按99.9%的可靠性要求,能否認為“成績與班級有關系”;
(3)若按下面的方法從甲班優秀的學生中抽取一人:把甲班優秀的10名學生從2到11進行編號,先后兩次拋擲一枚均勻的骰子,出現的點數之和為被抽取人的序號。試求抽到9號或10號的概率。
參考公式與臨界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,其前
,其前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求證:數列
),求證:數列![]() 是等比數列;
是等比數列;
⑵若數列![]() 是等比數列,求
是等比數列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求證:數列
,求證:數列![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知復數z滿足|z|![]() ,z的實部大于0,z2的虛部為2.
,z的實部大于0,z2的虛部為2.
(1)求復數z;
(2)設復數z,z2,z﹣z2之在復平面上對應的點分別為A,B,C,求(![]() )
)![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
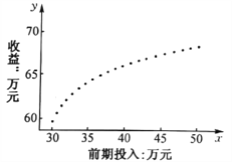
【題目】某互聯網公司為了確定下一季度的前期廣告投入計劃,收集了近期前期廣告投入量![]() (單位:萬元)和收益
(單位:萬元)和收益![]() (單位:萬元)的數據。對這些數據作了初步處理,得到了下面的散點圖(共
(單位:萬元)的數據。對這些數據作了初步處理,得到了下面的散點圖(共![]() 個數據點)及一些統計量的值.為了進一步了解廣告投入量
個數據點)及一些統計量的值.為了進一步了解廣告投入量![]() 對收益
對收益![]() 的影響,公司三位員工①②③對歷史數據進行分析,查閱大量資料,分別提出了三個回歸方程模型:
的影響,公司三位員工①②③對歷史數據進行分析,查閱大量資料,分別提出了三個回歸方程模型:
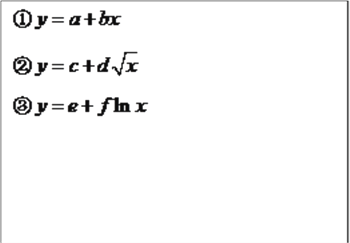
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根據![]() ,
, ![]() ,參考數據:
,參考數據: ![]() ,
, ![]() .
.
(1)根據散點圖判斷,哪一位員工提出的模型不適合用來描述![]() 與
與![]() 之間的關系?簡要說明理由.
之間的關系?簡要說明理由.
(2)根據(1)的判斷結果及表中數據,在余下兩個模型中分別建立收益![]() 關于投入量
關于投入量![]() 的關系,并從數據相關性的角度考慮,在余下兩位員工提出的回歸模型中,哪一個是最優模型(即更適宜作為收益
的關系,并從數據相關性的角度考慮,在余下兩位員工提出的回歸模型中,哪一個是最優模型(即更適宜作為收益![]() 的回歸方程)?說明理由;
的回歸方程)?說明理由;
附:對于一組數據![]() ,
, ![]() ,…,
,…, ![]() ,其回歸直線
,其回歸直線![]() 的斜率、截距的最小二乘估計以及相關系數分別為:
的斜率、截距的最小二乘估計以及相關系數分別為:
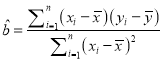 ,
, ![]() ,
, 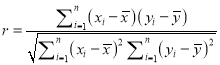 ,
,
其中![]() 越接近于
越接近于![]() ,說明變量
,說明變量![]() 與
與![]() 的線性相關程度越好.
的線性相關程度越好.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】求滿足下列條件的橢圓或雙曲線的標準方程:
(1)橢圓的焦點在![]() 軸上,焦距為4,且經過點
軸上,焦距為4,且經過點![]() ;
;
(2)雙曲線的焦點在![]() 軸上,右焦點為
軸上,右焦點為![]() ,過
,過![]() 作重直于
作重直于![]() 軸的直線交雙曲線于
軸的直線交雙曲線于![]() ,
,![]() 兩點,且
兩點,且![]() ,離心率為
,離心率為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 及點
及點![]() ,若直線
,若直線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,且
,且![]() (
( ![]() 為坐標原點),橢圓
為坐標原點),橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于不同的兩點
于不同的兩點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求![]() 的單調遞增區間.
的單調遞增區間.
(2)在ΔABC中,角A,B,C所對的邊分別為a,b,c,若f(A)=1,c=10,cosB=![]() ,求ΔABC的中線AD的長.
,求ΔABC的中線AD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com