
【題目】在平面直角坐標系![]() 中,
中,![]() 為拋物線
為拋物線![]() 上不同的兩點,且
上不同的兩點,且![]() ,點
,點![]()
![]() 且
且![]() 于點
于點![]() .
.
(1)求![]() 的值;
的值;
(2)過![]() 軸上一點
軸上一點 ![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 在
在![]() 的準線上的射影分別為
的準線上的射影分別為![]() ,
,![]() 為
為![]() 的焦點,若
的焦點,若![]() ,求
,求![]() 中點
中點![]() 的軌跡方程.
的軌跡方程.
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線C:![]() ,過拋物線焦點F的直線交拋物線C于A,B兩點,P是拋物線外一點,連接
,過拋物線焦點F的直線交拋物線C于A,B兩點,P是拋物線外一點,連接![]() ,
,![]() 分別交拋物線于點C,D,且
分別交拋物線于點C,D,且![]() ,設
,設![]() ,
,![]() 的中點分別為M,N.
的中點分別為M,N.
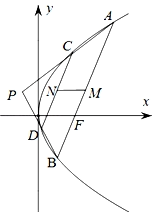
(1)求證:![]() 軸;
軸;
(2)若![]() ,求
,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AB∥CD,AD=DC=BC=1,∠ABC=60°,四邊形ACFE為矩形,平面ACFE⊥平面ABCD,CF=1.
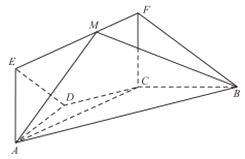
(1)證明:BC⊥平面ACFE;
(2)設點M在線段EF上運動,平面MAB與平面FCB所成銳二面角為θ,求cosθ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直角三角形ABC的三個頂點都在橢圓![]() 上,其中A(0,1)為直角頂點.若該三角形的面積的最大值為
上,其中A(0,1)為直角頂點.若該三角形的面積的最大值為![]() ,則實數a的值為_____.
,則實數a的值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對有![]() 個元素的總體
個元素的總體![]() 進行抽樣,先將總體分成兩個子總體
進行抽樣,先將總體分成兩個子總體![]() 和
和![]() (
(![]() 是給定的正整數,且
是給定的正整數,且![]() ),再從每個子總體中各隨機抽取2個元素組成樣本.用
),再從每個子總體中各隨機抽取2個元素組成樣本.用![]() 表示元素
表示元素![]() 和
和![]() 同時出現在樣本中的概率.
同時出現在樣本中的概率.
(1)求![]() 的表達式(用
的表達式(用![]() ,
,![]() 表示);
表示);
(2)求所有![]() 的和.
的和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a![]() ,c
,c![]() ,________.(補充條件)
,________.(補充條件)
(1)求△ABC的面積;
(2)求sin(A+B).
從①b=4,②cosB![]() ,③sinA
,③sinA![]() 這三個條件中任選一個,補充在上面問題中并作答.
這三個條件中任選一個,補充在上面問題中并作答.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com