
【題目】在一次數學競賽中,30名參賽學生的成績(百分制)的莖葉圖如圖所示:若將參賽學生按成績由高到低編為1﹣30號,再用系統抽樣法從中抽取6人,則其中抽取的成績在[77,90]內的學生人數為( ) 
A.2
B.3
C.4
D.5
【答案】C
【解析】解:由莖葉圖可得30名學生的成績如下:
94,94,92,92,91;90,90,88,88,87;
87,85,84,83,83;83,83,82,82,82;
81,80,78,78,77;73,72,71,70,70.
若用系統抽樣,則需分6段,則第2,3,4,5區間段內抽取的學生成績符合題意,有4人.
故選:C.
【考點精析】解答此題的關鍵在于理解莖葉圖的相關知識,掌握莖葉圖又稱“枝葉圖”,它的思路是將數組中的數按位數進行比較,將數的大小基本不變或變化不大的位作為一個主干(莖),將變化大的位的數作為分枝(葉),列在主干的后面,這樣就可以清楚地看到每個主干后面的幾個數,每個數具體是多少.


科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() 的焦距為2
的焦距為2![]() ,一條準線方程為x=
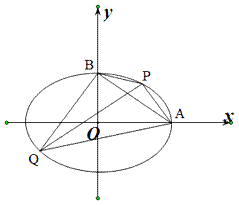
,一條準線方程為x=![]() ,A,B分別為橢圓的右頂點和上頂點,點P,Q在的橢圓上,且點P在第一象限.
,A,B分別為橢圓的右頂點和上頂點,點P,Q在的橢圓上,且點P在第一象限.
(1)求橢圓E的標準方程;
(2)若點P,Q關于坐標原點對稱,且PQ⊥AB,求四邊形ABCD的面積;
(3)若AP,BQ的斜率互為相反數,求證:PQ斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題 ![]() 方程
方程 ![]() 有兩個不相等的負實根,
有兩個不相等的負實根,
命題 ![]() 不等式
不等式 ![]() 的解集為
的解集為 ![]() ,
,
(1)若![]() 為真命題,求
為真命題,求 ![]() 的取值范圍.
的取值范圍.
(2)若 ![]() 為真命題,
為真命題,![]() 為假命題,求
為假命題,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中內動點P(x,y)到圓F:x2+(y﹣1)2=1的圓心F的距離比它到直線y=﹣2的距離小1.
(1)求動點P的軌跡方程;
(2)設點P的軌跡為曲線E,過點F的直線l的斜率為k,直線l交曲線E于A,B兩點,交圓F于C,D兩點(A,C兩點相鄰).
①若 ![]() =t
=t ![]() ,當t∈[1,2]時,求k的取值范圍;
,當t∈[1,2]時,求k的取值范圍;
②過A,B兩點分別作曲線E的切線l1 , l2 , 兩切線交于點N,求△ACN與△BDN面積之積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數f(x)給出定義:
設f′(x)是函數y=f(x)的導數,f″(x)是函數f′(x)的導數,若方程f″(x)=0有實數解x0 , 則稱點(x0 , f(x0))為函數y=f(x)的“拐點”.
某同學經過探究發現:任何一個三次函數f(x)=ax3+bx2+cx+d(a≠0)都有“拐點”;任何一個三次函數都有對稱中心,且“拐點”就是對稱中心.給定函數 ![]() ,請你根據上面探究結果,計算
,請你根據上面探究結果,計算![]() = .
= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的長軸長是短軸長的
的長軸長是短軸長的![]() 倍,右焦點為
倍,右焦點為![]() ,點
,點![]() 分別是該橢圓的上、下頂點,點
分別是該橢圓的上、下頂點,點![]() 是直線
是直線![]() 上的一個動點(與
上的一個動點(與![]() 軸交點除外),直線
軸交點除外),直線![]() 交橢圓于另一點
交橢圓于另一點![]() ,記直線
,記直線![]() ,
, ![]() 的斜率分別為
的斜率分別為![]()

(1)當直線![]() 過點
過點![]() 時,求
時,求![]() 的值;
的值;
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com