【題目】已知
為坐標原點，橢圓
的右焦點為
，過的直線
與
相交于
兩點，點
滿足
.
（1）當的傾斜角為
時，求直線
的方程；
（2）試探究在
軸上是否存在定點
，使得
為定值？若存在，求出點的坐標；若不存在，請說明理由.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列四個命題中，正確命題的個數(shù)有（ ）
①
，
②命題“
，
”的否定是“
，
”
③“若
，則
，
中至少有一個不小于2”的逆命題是真命題
④復(fù)數(shù)
，則
的充分不必要條件是
A.1B.2C.3D.4
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，四棱錐
的底面是邊長為2的正方形，平面
平面
，
，
．
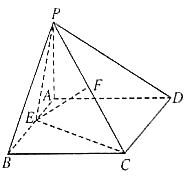
（1）求證：平面平面
；
（2）設(shè)
為
的中點，問邊
上是否存在一點
，使
平面
，并求此時點到平面的距離．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某花卉企業(yè)引進了數(shù)百種不同品種的康乃馨，通過試驗田培育，得到了這些康乃馨種子在當?shù)丨h(huán)境下的發(fā)芽率，并按發(fā)芽率分為
組：
、
、
、
加以統(tǒng)計，得到如圖所示的頻率分布直方圖．企業(yè)對康乃馨的種子進行分級，將發(fā)芽率不低于
的種子定為“
級”，發(fā)芽率低于但不低于
的種子定為“
級”，發(fā)芽率低于的種子定為“
級”．
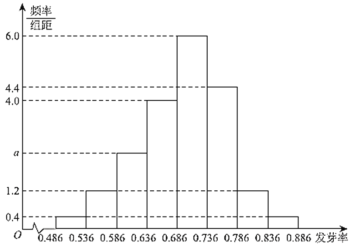
（Ⅰ）現(xiàn)從這些康乃馨種子中隨機抽取一種，估計該種子不是“級”種子的概率；
（Ⅱ）該花卉企業(yè)銷售花種，且每份“級”、“級”、“級”康乃馨種子的售價分別為
元、
元、
元．某人在市場上隨機購買了該企業(yè)銷售的康乃馨種子兩份，共花費
元，以頻率為概率，求的分布列和數(shù)學(xué)期望；
（Ⅲ）企業(yè)改進了花卉培育技術(shù)，使得每種康乃馨種子的發(fā)芽率提高到原來的
倍，那么對于這些康乃馨的種子，與舊的發(fā)芽率數(shù)據(jù)的方差相比，技術(shù)改進后發(fā)芽率數(shù)據(jù)的方差是否發(fā)生變化？若發(fā)生變化，是變大了還是變小了？（結(jié)論不需要證明）．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某建材商場國慶期間搞促銷活動，規(guī)定：如果顧客選購物品的總金額不超過600元，則不享受任何折扣優(yōu)惠；如果顧客選購物品的總金額超過600元，則超過600元部分享受一定的折扣優(yōu)惠，折扣優(yōu)惠按下表累計計算.
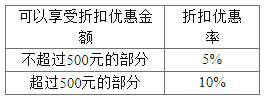
某人在此商場購物獲得的折扣優(yōu)惠金額為30元，則他實際所付金額為____元．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】從某企業(yè)生產(chǎn)的某種產(chǎn)品中抽取100件，測量這些產(chǎn)品的一項質(zhì)量指標值，由測量表得如下頻數(shù)分布表：
質(zhì)量指標值分組 | [75，85) | [85，95) | [95，105) | [105，115) | [115，125) |
頻數(shù) | 6 | 26 | 38 | 22 | 8 |
（I）在答題卡上作出這些數(shù)據(jù)的頻率分布直方圖：
（II）估計這種產(chǎn)品質(zhì)量指標值的平均數(shù)及方差（同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表）；
（III）根據(jù)以上抽樣調(diào)查數(shù)據(jù)，能否認為該企業(yè)生產(chǎn)的這種產(chǎn)品符合“質(zhì)量指標值不低于95的產(chǎn)品至少要占全部產(chǎn)品的80%”的規(guī)定？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，曲線
在點
處的切線方程是
.
（Ⅰ）求實數(shù)
，
的值;
（Ⅱ）若函數(shù)
有兩個不同的零點
，
，求證：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若拋物線
的焦點為
，
是坐標原點，
為拋物線上的一點，向量
與
軸正方向的夾角為60°，且
的面積為
.
（1）求拋物線
的方程；
（2）若拋物線的準線與軸交于點
，點
在拋物線上，求當
取得最大值時，直線
的方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知點
，
，拋物線
的焦點
為線段
中點.
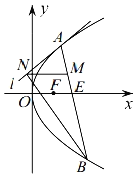
（1）求拋物線
的方程；
（2）過點
的直線交拋物線于
兩點，
，過點
作拋物線的切線
，
為切線上的點，且
軸，求
面積的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
