
【題目】如圖,在長方體![]() 中,
中,![]() 、
、![]() 分別是棱
分別是棱![]() ,
,![]()
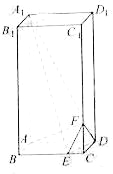
上的點,![]() ,
,![]()
(1) 求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(2) 證明![]()
![]() 平面
平面![]()
![]()
(3) 求二面角![]() 的正弦值.
的正弦值.
【答案】(1)![]() ,(2)見解析(3)
,(2)見解析(3)![]()
【解析】
方法一:如圖所示,建立空間直角坐標系,
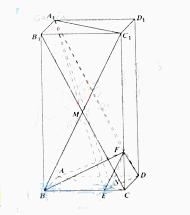
點A為坐標原點,設![]() ,依題意得
,依題意得![]() ,
,
![]() ,
,![]() ,
,![]()
(1) 解:易得![]() ,
,![]()
于是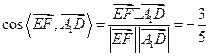
所以異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]()
(2) 證明:已知![]() ,
,![]() ,
,![]()
于是![]() ·
·![]() =0,
=0,![]() ·
·![]() =0.因此,
=0.因此,![]() ,
,![]() ,又
,又![]()
所以![]() 平面
平面![]()
(3)解:設平面![]() 的法向量
的法向量![]() ,則
,則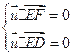 ,即
,即
不妨令X=1,可得![]() .由(2)可知,
.由(2)可知,![]() 為平面
為平面![]() 的一個法向量.
的一個法向量.
于是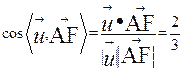 ,從而
,從而![]()
所以二面角![]() 的正弦值為
的正弦值為![]()
方法二:(1)解:設AB=1,可得AD=2,AA1=4,CF=1.CE=![]()
鏈接B1C,BC1,設B1C與BC1交于點M,易知A1D∥B1C,由![]() ,可知EF∥BC1.故
,可知EF∥BC1.故![]() 是異面直線EF與A1D所成的角,易知BM=CM=
是異面直線EF與A1D所成的角,易知BM=CM=![]() ,所以
,所以![]() ,所以異面直線FE與A1D所成角的余弦值為
,所以異面直線FE與A1D所成角的余弦值為![]()
(2)證明:連接AC,設AC與DE交點N 因為![]() ,所以
,所以![]() ,從而
,從而![]() ,又由于
,又由于![]() ,所以
,所以![]() ,故AC⊥DE,又因為CC1⊥DE且
,故AC⊥DE,又因為CC1⊥DE且![]() ,所以DE⊥平面ACF,從而AF⊥DE.
,所以DE⊥平面ACF,從而AF⊥DE.
連接BF,同理可證B1C⊥平面ABF,從而AF⊥B1C,所以AF⊥A1D因為![]() ,所以AF⊥平面A1ED
,所以AF⊥平面A1ED
(3)解:連接A1N.FN,由(2)可知DE⊥平面ACF,又NF![]() 平面ACF, A1N
平面ACF, A1N![]() 平面ACF,所以DE⊥NF,DE⊥A1N,故
平面ACF,所以DE⊥NF,DE⊥A1N,故![]() 為二面角A1-ED-F的平面角
為二面角A1-ED-F的平面角
易知![]() ,所以
,所以![]() ,又
,又![]() 所以
所以![]() ,在
,在![]()
![]()
連接A1C1,A1F 在![]()
![]() .所以
.所以![]()
所以二面角A1-DE-F正弦值為![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,焦距為
,焦距為![]() .斜率為k的直線l與橢圓M有兩個不同的交點A,B.
.斜率為k的直線l與橢圓M有兩個不同的交點A,B.
(Ⅰ)求橢圓M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)設![]() ,直線PA與橢圓M的另一個交點為C,直線PB與橢圓M的另一個交點為D.若C,D和點
,直線PA與橢圓M的另一個交點為C,直線PB與橢圓M的另一個交點為D.若C,D和點![]() 共線,求k.
共線,求k.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】冬天的北方室外溫度極低,若輕薄保暖的石墨烯發熱膜能用在衣服上,可愛的醫務工作者行動會更方便.石墨烯發熱膜的制作:從石墨中分離出石墨烯,制成石墨烯發熱膜.從石墨分離石墨烯的一種方法是化學氣相沉積法,使石墨升華后附著在材料上再結晶.現在有![]() 材料、
材料、![]() 材料供選擇,研究人員對附著在
材料供選擇,研究人員對附著在![]() 材料、
材料、![]() 材料上再結晶各做了50次試驗,得到如下等高條形圖.
材料上再結晶各做了50次試驗,得到如下等高條形圖.
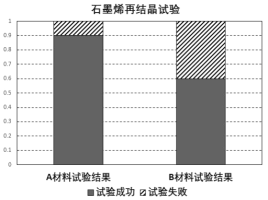
(1)根據上面的等高條形圖,填寫如下列聯表,判斷是否有99%的把握認為試驗成功與材料有關?
|
| 合計 | |
成功 | |||
不成功 | |||
合計 |
(2)研究人員得到石墨烯后,再制作石墨烯發熱膜有三個環節:①透明基底及![]() 膠層;②石墨烯層;③表面封裝層.第一、二環節生產合格的概率均為
膠層;②石墨烯層;③表面封裝層.第一、二環節生產合格的概率均為![]() ,第三個環節生產合格的概率為
,第三個環節生產合格的概率為![]() ,且各生產環節相互獨立.已知生產1噸的石墨烯發熱膜的固定成本為1萬元,若生產不合格還需進行修復,第三個環節的修復費用為3000元,其余環節修復費用均為1000元.如何定價,才能實現每生產1噸石墨烯發熱膜獲利可達1萬元以上的目標?
,且各生產環節相互獨立.已知生產1噸的石墨烯發熱膜的固定成本為1萬元,若生產不合格還需進行修復,第三個環節的修復費用為3000元,其余環節修復費用均為1000元.如何定價,才能實現每生產1噸石墨烯發熱膜獲利可達1萬元以上的目標?
附:參考公式: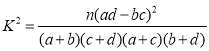 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)選修4—4,坐標系與參數方程
已知曲線![]() ,直線
,直線![]() :
:![]() (
(![]() 為參數).
為參數).
(I)寫出曲線![]() 的參數方程,直線
的參數方程,直線![]() 的普通方程;
的普通方程;
(II)過曲線![]() 上任意一點
上任意一點![]() 作與
作與![]() 夾角為
夾角為![]() 的直線,交
的直線,交![]() 于點
于點![]() ,
,![]() 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn,若S9=81,a3+a5=14.
(1)求數列{an}的通項公式;
(2)設bn=![]() ,若{bn}的前n項和為Tn,證明:Tn<
,若{bn}的前n項和為Tn,證明:Tn<![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=2ax2+2bx,若存在實數x0∈(0,t),使得對任意不為零的實數a,b均有f(x0)=a+b成立,則t的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程選講
在平面直角坐標系中,以原點為極點,以![]() 軸非負半軸為極軸建立極坐標系, 已知曲線
軸非負半軸為極軸建立極坐標系, 已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出曲線![]() 和直線
和直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 過點
過點![]() 與曲線
與曲線![]() 交于不同兩點
交于不同兩點![]() ,
,![]() 的中點為
的中點為![]() ,
,![]() 與
與![]() 的交點為
的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 的左右頂點,
的左右頂點,![]() 點為橢圓
點為橢圓![]() 上一點,點
上一點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,且
,且![]() .
.
(1)若橢圓![]() 經過圓
經過圓![]() 的圓心,求橢圓
的圓心,求橢圓![]() 的方程;
的方程;
(2)在(1)的條件下,若過點![]() 的直線與橢圓
的直線與橢圓![]() 相交于不同的
相交于不同的![]() 兩點,設
兩點,設![]() 為橢圓
為橢圓![]() 上一點,且滿足
上一點,且滿足![]() (
(![]() 為坐標原點),當
為坐標原點),當![]() 時,求實數
時,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代有著輝煌的數學研究成果,其中的《周髀算經》、《九章算術》、《海島算經》、《孫子算經》、《緝古算經》,有豐富多彩的內容,是了解我國古代數學的重要文獻,這5部專著中有3部產生于漢、魏、晉、南北朝時期,某中學擬從這5部專著中選擇2部作為“數學文化”校本課程學習內容,則所選2部專著中至少有一部是漢、魏、晉、南北朝時期專著的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com