
【題目】已知在等差數列![]() 中,
中, ![]() 為其前
為其前![]() 項和,
項和, ![]() ,
,![]() ;等比數列
;等比數列![]() 的前
的前![]() 項和
項和![]() .
.
(I)求數列![]() ,
, ![]() 的通項公式;
的通項公式;
(II)設![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
科目:高中數學 來源: 題型:
【題目】某上市股票在30天內每股的交易價格P(元)與時間t(天)組成有序數對(t,P),點(t,P)落在圖中的兩條線段上(如圖).該股票在30天內(包括第30天)的日交易量Q(萬股)與時間t(天)的函數關系式為Q=40﹣t(0≤t≤30且t∈N). 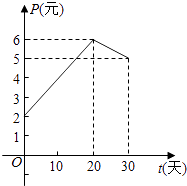
(1)根據提供的圖象,求出該種股票每股的交易價格P(元)與時間t(天)所滿足的函數關系式;
(2)用y(萬元)表示該股票日交易額(日交易額=日交易量×每股的交易價格),寫出y關于t的函數關系式,并求出這30天中第幾天日交易額最大,最大值為多少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐V﹣ABC中,平面VAB⊥平面ABC,△VAB為等邊三角形,AC⊥BC且AC=BC= ![]() ,O,M分別為AB,VA的中點.
,O,M分別為AB,VA的中點. 
(1)求證:VB∥平面MOC;
(2)求證:平面MOC⊥平面VAB
(3)求三棱錐V﹣ABC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2﹣2x﹣2ay+a2﹣24=0(a∈R)的圓心在直線2x﹣y=0上.
(1)求實數a的值;
(2)求圓C與直線l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R)相交弦長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ).
).
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若不等式![]() 對任意
對任意![]() 恒成立.(i)求實數
恒成立.(i)求實數![]() 的取值范圍;(ii)試比較
的取值范圍;(ii)試比較![]() 與
與![]() 的大小,并給出證明(
的大小,并給出證明(![]() 為自然對數的底數,
為自然對數的底數, ![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的首項a1=1,公差d>0,且第2項、第5項、第14項分別是等比數列{bn}的第2項、第3項、第4項.
(1)求數列{an}與{bn}的通項公式;
(2)設數列{cn}對n∈N*均有 ![]() =an+1成立,求c1+c2+c3+…+c2016 .
=an+1成立,求c1+c2+c3+…+c2016 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com