【題目】已知直線l的方程為3x+4y﹣12=0，求直線l'的方程，使得：
（1）l'與l平行，且過點（﹣1，3）；
（2）l'與l垂直，且l'與兩軸圍成的三角形面積為4．
【答案】
（1）解：∵直線l的方程為3x+4y﹣12=0
∴直線l斜率為﹣ 
∵l'與l平行
∴直線l'斜率為﹣
∴直線l'的方程為y﹣3=﹣ （x+1）即3x+4y﹣9=0
（2）解：∵l′⊥l，∴kl′= 
．
設l′在x軸上截距為b，則l′在y軸上截距為﹣ b，
由題意可知，S= 
|b||﹣ b|=4，∴b=± 
．
∴直線l′：y= x+ ，或y= x﹣
【解析】（1）根據平行直線的斜率相等，先求出斜率，點斜式求得直線方程．（2）根據垂直關系求出直線的斜率，得到它在坐標軸上的截距，根據與兩坐標軸圍成的三角形面積為4 求出截距，即得直線方程．
【考點精析】掌握點斜式方程是解答本題的根本，需要知道直線的點斜式方程：直線
經過點
，且斜率為
則：
．
科目：高中數學 來源： 題型：
【題目】如圖1，已知在菱形
中， 
， 
為
的中點，現將四邊形
沿
折起至
，如圖2.
（1）求證： 
面
；
（2）若二面角
的大小為
，求平面
與平面
所成銳二面角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廠商調查甲、乙兩種不同型號電視機在10個賣場的銷售量（單位：臺），并根據這10個賣場的銷售情況，得到如圖所示的莖葉圖. 為了鼓勵賣場，在同型號電視機的銷售中，該廠商將銷售量高于數據平均數的賣場命名為該型號電視機的“星級賣場”．
（1）求在這10個賣場中，甲型號電視機的“星級賣場”的個數；
（2）若在這10個賣場中，乙型號電視機銷售量的平均數為26.7，求a>b的概率；
（3）若a=1，記乙型號電視機銷售量的方差為
，根據莖葉圖推斷b為何值時，達到最值．
（只需寫出結論）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）= 
，其中向量 =（2cosx，1）， =（cosx， 
sin2x），x∈R．
（1）求f（x）的單調遞增區間；
（2）在△ABC中，a，b，c分別是角A，B，C的對邊，已知f（A）=2，b=1，△ABC的面積為 
，求c的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據國家環保部新修訂的《環境空氣質量標準》規定：居民區
的年平均濃度不得超過35微克/立方米， 
的24小時平均濃度不得超過75微克/立方米．我市環保局隨機抽取了一居民區2016年30天
的24小時平均濃度（單位：微克/立方米）的監測數據，將這30天的測量結果繪制成樣本頻率分布直方圖如圖．
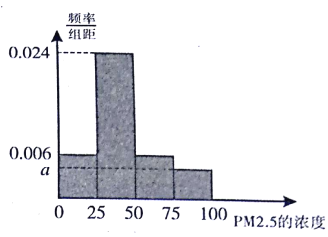
（Ⅰ）求圖中
的值；
（Ⅱ）由頻率分布直方圖中估算樣本平均數，并根據樣本估計總體的思想，從
的年平均濃度考慮，判斷該居民區的環境質量是否需要改善？并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn ， 且Sn=n﹣5an﹣85，n∈N+ ．
（1）求an ．
（2）求數列{Sn}的通項公式，并求出n為何值時，Sn取得最小值？并說明理由．（參考數據：lg 2≈0.3，lg 3≈0.48）．
查看答案和解析>>
科目：高中數學 來源： 題型：
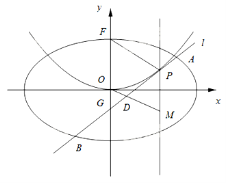
【題目】【2016高考山東理數】平面直角坐標系
中，橢圓C：
的離心率是
，拋物線E：
的焦點F是C的一個頂點.
（I）求橢圓C的方程；
（II）設P是E上的動點，且位于第一象限，E在點P處的切線
與C交與不同的兩點A，B，線段AB的中點為D，直線OD與過P且垂直于x軸的直線交于點M.
（i）求證：點M在定直線上;
（ii）直線與y軸交于點G，記
的面積為
，
的面積為
，求
的最大值及取得最大值時點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
