
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60][60,70][70,80][80,90][90,100].

(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示,求數學成績在[50,90)之外的人數.

 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)(x∈R)滿足f(1)=1,且f(x)的導函數f′(x)< ![]() ,則不等式f(x2)<
,則不等式f(x2)< ![]() +
+ ![]() 的解集為( )
的解集為( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣∞,﹣1)∪(1,+∞)??
C.(﹣1,1)
D.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和Sn滿足2Sn=3an﹣1,其中n∈N* .
(1)求數列{an}的通項公式;
(2)設anbn= ![]() ,求數列{bn}的前n項和為Tn .
,求數列{bn}的前n項和為Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正三棱柱![]() 的所有棱長都相等,
的所有棱長都相等,![]() 分別為
分別為![]() 的中點.現有下列四個結論:
的中點.現有下列四個結論:
![]() :
:![]() ;
; ![]() :
:![]() ;
;
![]() :
:![]() 平面
平面![]() ;
; ![]() :異面直線
:異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
其中正確的結論是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
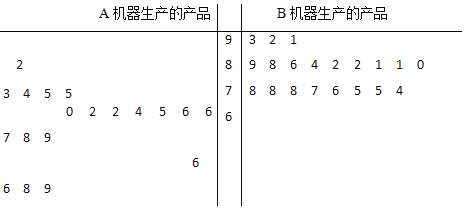
【題目】某工廠有兩臺不同機器A和B生產同一種產品各10萬件,現從各自生產的產品中分別隨機抽取20件,進行品質鑒定,鑒定成績的莖葉圖如圖所示:
該產品的質量評價標準規定:鑒定成績達到![]() 的產品,質量等級為優秀;鑒定成績達到
的產品,質量等級為優秀;鑒定成績達到![]() 的產品,質量等級為良好;鑒定成績達到
的產品,質量等級為良好;鑒定成績達到![]() 的產品,質量等級為合格
的產品,質量等級為合格![]() 將這組數據的頻率視為整批產品的概率.
將這組數據的頻率視為整批產品的概率.
![]() Ⅰ
Ⅰ![]() 從等級為優秀的樣本中隨機抽取兩件,記X為來自B機器生產的產品數量,寫出X的分布列,并求X的數學期望;
從等級為優秀的樣本中隨機抽取兩件,記X為來自B機器生產的產品數量,寫出X的分布列,并求X的數學期望;
![]() Ⅱ
Ⅱ![]() 完成下列
完成下列![]() 列聯表,以產品等級是否達到良好以上
列聯表,以產品等級是否達到良好以上![]() 含良好
含良好![]() 為判斷依據,判斷能不能在誤差不超過
為判斷依據,判斷能不能在誤差不超過![]() 的情況下,認為B機器生產的產品比A機器生產的產品好;
的情況下,認為B機器生產的產品比A機器生產的產品好;
A生產的產品 | B生產的產品 | 合計 | |
良好以上 | |||
合格 | |||
合計 |
![]() 已知優秀等級產品的利潤為12元
已知優秀等級產品的利潤為12元![]() 件,良好等級產品的利潤為10元
件,良好等級產品的利潤為10元![]() 件,合格等級產品的利潤為5元
件,合格等級產品的利潤為5元![]() 件,A機器每生產10萬件的成本為20萬元,B機器每生產10萬件的成本為30萬元;該工廠決定:按樣本數據測算,兩種機器分別生產10萬件產品,若收益之差達到5萬元以上,則淘汰收益低的機器,若收益之差不超過5萬元,則仍然保留原來的兩臺機器
件,A機器每生產10萬件的成本為20萬元,B機器每生產10萬件的成本為30萬元;該工廠決定:按樣本數據測算,兩種機器分別生產10萬件產品,若收益之差達到5萬元以上,則淘汰收益低的機器,若收益之差不超過5萬元,則仍然保留原來的兩臺機器![]() 你認為該工廠會仍然保留原來的兩臺機器嗎?
你認為該工廠會仍然保留原來的兩臺機器嗎?
附:![]() 獨立性檢驗計算公式:
獨立性檢驗計算公式:![]() .
.
![]() 臨界值表:
臨界值表:
|
|
|
|
|
|
k |
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,焦距為
,焦距為![]() .斜率為k的直線l與橢圓M有兩個不同的交點A,B.
.斜率為k的直線l與橢圓M有兩個不同的交點A,B.
(Ⅰ)求橢圓M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)設![]() ,直線PA與橢圓M的另一個交點為C,直線PB與橢圓M的另一個交點為D.若C,D和點
,直線PA與橢圓M的另一個交點為C,直線PB與橢圓M的另一個交點為D.若C,D和點![]() 共線,求k.
共線,求k.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等比數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差數列,數列
成等差數列,數列![]() 滿足
滿足![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,若對任意
,若對任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+bx2+cx﹣1當x=﹣2時有極值,且在x=﹣1處的切線的斜率為﹣3.
(1)求函數f(x)的解析式;
(2)求函數f(x)在區間[﹣1,2]上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,D,E分別為棱AB,BC的中點,點F在側棱B1B上,且B1E⊥C1F,A1C1⊥B1C1.
(1)求證:DE∥平面A1C1F;
(2)求證:B1E⊥平面A1C1F

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com