
【題目】如圖,將邊長為2的正方形![]() 沿對角線
沿對角線![]() 折疊,使得平面
折疊,使得平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() .
.
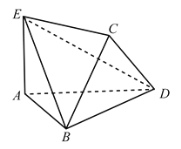
(1)若![]() ,求直線
,求直線![]() 與直線
與直線![]() 所成的角;
所成的角;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的長度.
的長度.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由題意可知,AB⊥AD, AE⊥平面ABD,以A為原點,AB、AD、AE所在直線分別為x軸,y軸,z軸,建立空間直角坐標系,作![]() ,垂足為
,垂足為![]() ,可得
,可得![]() ,得到C點坐標,利用向量法能求得
,得到C點坐標,利用向量法能求得![]() ,即可得到所求角.
,即可得到所求角.
(2)設![]() 的長度為
的長度為![]() ,則
,則![]() ,由題意知
,由題意知![]() 平面
平面![]() ,可得平面
,可得平面![]() 的一個法向量為
的一個法向量為![]() ,再求得平面
,再求得平面![]() 的法向量為
的法向量為![]() ,
,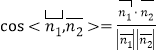
![]() ,解得a即可.
,解得a即可.
∵正方形![]() 邊長為2 ∴
邊長為2 ∴![]() ,
,![]() ,
,![]()
又![]() 平面
平面![]() ,∴以點
,∴以點![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系.
軸建立空間直角坐標系.
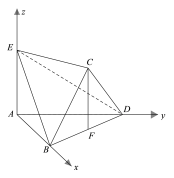
作![]() ,垂足為
,垂足為![]() ,∵平面
,∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ∵
∵![]() ∴點
∴點![]() 為
為![]() 的中點,
的中點,![]() ,
,
(1)∵![]()
∴![]() ,
,![]() ,
,![]() ,,
,,![]()
∴![]() ,
,![]() ∴
∴![]()
∴![]() ∴直線
∴直線![]() 與直線
與直線![]() 所成角為
所成角為![]() ;
;
(2)設![]() 的長度為
的長度為![]() ,則
,則![]()
∵![]() 平面
平面![]() ∴平面
∴平面![]() 的一個法向量為
的一個法向量為![]()
設平面![]() 的法向量為
的法向量為![]() ,又
,又![]() ,
,![]()
∴![]() ,
,![]() ∴
∴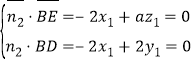 ,解得:
,解得: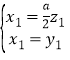 ,取
,取![]() ,則
,則![]() ,
,
∴平面![]() 的一個法向量為
的一個法向量為![]()
∴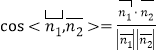
![]()
∵二面角![]() 的大小為
的大小為![]() ∴
∴![]() ,解得:
,解得:![]()
∴![]() 的長度為
的長度為![]() .
.


科目:高中數學 來源: 題型:
【題目】我國于2015年10月宣布實施普遍二孩政策,為了解戶籍、性別對生育二胎選擇傾向的影響,某地從育齡群體中隨機抽取了容量為140的調查樣本,其中城鎮戶籍與農村戶籍各70人;男性60人,女性80人,繪制的不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數比例如圖所示,其中陰影部分表示傾向選擇生育二胎的對應比例,則下列敘述正確的是( )
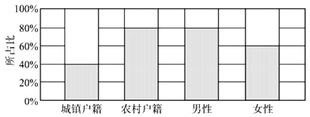
A.是否傾向選擇生育二胎與戶籍有關
B.是否傾向選擇生育二胎與性別有關
C.調查樣本里面傾向選擇生育二胎的人群中,男性人數少于女性人數
D.傾向選擇不生育二胎的人群中,農村戶籍人數多于城鎮戶籍人數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為評估設備![]() 生產某種零件的性能,從設備
生產某種零件的性能,從設備![]() 生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
直徑 | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計 |
件數 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經計算,樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.
,以頻率值作為概率的估計值.
(1)由以往統計數據知,設備的性能根據以下不等式進行評判(![]() 表示相應事件的概率);①
表示相應事件的概率);①![]() ;②
;②![]() ;③
;③![]() ,評判規則為:若同時滿足上述三個不等式,則設備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁.為評判一臺設備
,評判規則為:若同時滿足上述三個不等式,則設備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁.為評判一臺設備![]() 的性能,從該設備加工的零件中任意抽取一件,記其直徑為
的性能,從該設備加工的零件中任意抽取一件,記其直徑為![]() ,試判斷設備
,試判斷設備![]() 的性能等級
的性能等級
(2)將直徑小于等于![]() 或直徑大于
或直徑大于![]() 的零件認為是次品.
的零件認為是次品.
(i)若從設備![]() 的生產流水線上隨意抽取2件零件,求恰有一件次品的概率;
的生產流水線上隨意抽取2件零件,求恰有一件次品的概率;
(ii)若從樣本中隨意抽取2件零件,計算其中次品個數![]() 分布列和數學期望
分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記無窮數列![]() 的前n項中最大值為
的前n項中最大值為![]() ,最小值為
,最小值為![]() ,令
,令![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() .
.
(1)若數列![]() 是首項為2,公比為2的等比數列,求
是首項為2,公比為2的等比數列,求![]() ;
;
(2)若數列![]() 是等差數列,試問數列
是等差數列,試問數列![]() 是否也一定是等差數列?若是,請證明;若不是,請舉例說明;
是否也一定是等差數列?若是,請證明;若不是,請舉例說明;
(3)若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知甲、乙兩名工人在同樣條件下每天各生產100件產品,且每生產1件正品可獲利20元,生產1件次品損失30元,甲,乙兩名工人100天中出現次品件數的情況如表所示.
甲每天生產的次品數/件 | 0 | 1 | 2 | 3 | 4 |
對應的天數/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生產的次品數/件 | 0 | 1 | 2 | 3 |
對應的天數/天 | 30 | 25 | 25 | 20 |
(1)將甲每天生產的次品數記為![]() (單位:件),日利潤記為
(單位:件),日利潤記為![]() (單位:元),寫出
(單位:元),寫出![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)如果將統計的100天中產生次品量的頻率作為概率,記![]() 表示甲、乙兩名工人1天中各自日利潤不少于1950元的人數之和,求隨機變量
表示甲、乙兩名工人1天中各自日利潤不少于1950元的人數之和,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列命題:
①在線性回歸模型中,相關指數![]() 越接近于1,表示回歸效果越好;
越接近于1,表示回歸效果越好;
②兩個變量相關性越強,則相關系數r就越接近于1;
③在回歸直線方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 平均減少0.5個單位;
平均減少0.5個單位;
④兩個模型中殘差平方和越小的模型擬合的效果越好.
⑤回歸直線![]() 恒過樣本點的中心
恒過樣本點的中心![]() ,且至少過一個樣本點;
,且至少過一個樣本點;
⑥若![]() 的觀測值滿足
的觀測值滿足![]() ≥6.635,我們有99%的把握認為吸煙與患肺病有關系,那么在100個吸煙的人中必有99人患有肺病;
≥6.635,我們有99%的把握認為吸煙與患肺病有關系,那么在100個吸煙的人中必有99人患有肺病;
⑦從統計量中得知有95%的把握認為吸煙與患肺病有關系,是指有5%的可能性使得推斷出現錯誤. 其中正確命題的序號是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com