Question

【題目】某數學教師對所任教的兩個班級各抽取20名學生進行測試，分數分布如表：

分數區間	甲班頻率	乙班頻率
	0.1	0.2
	0.2	0.2
	0.3	0.3
	0.2	0.2
	0.2	0.1

（Ⅰ）若成績120分以上（含120分）為優秀，求從乙班參加測試的90分以上（含90分）的同學中，隨機任取2名同學，恰有1人為優秀的概率；

（Ⅱ）根據以上數據完成下面的×列聯表：

	優秀	不優秀	總計
甲班
乙班
總計

在犯錯概率小于0.1的前提下，你是否有足夠的把握認為學生的數學成績是否優秀與班級有關系？

參考公式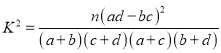：，其中

≥

Answer 1

【答案】（Ⅰ）；（Ⅱ）列聯表見解析，在犯錯概率小于的前提下，沒有足夠的把握認為學生的數學成績是否優秀與班級有關系．

【解析】

試題分析：（Ⅰ）乙班參加測試的 分以上的同學有 人，記為．成績優秀的記為．從這六名學生隨機抽取兩名的基本事件有個,恰有一位學生成績優秀的事件有共個；

（Ⅱ）由列聯表沒有足夠的把握．

試題解析：（Ⅰ）乙班參加測試的 分以上的同學有 人，記為．成績優秀的記為．從這六名學生隨機抽取兩名的基本事件有： , ,,,,,,,,,,,,,共 個設事件表示恰有一位學生成績優秀，符合要求的事件有,,,,,,,共 個所以

（Ⅱ） 列聯表如下

	優秀	不優秀	總計
甲班		/td>
乙班
總計

在犯錯概率小于的前提下，沒有足夠的把握說明學生的數學成績是否優秀與班級有關系．