
【題目】已知數(shù)列{bn}的前n項(xiàng)和是Sn , 且bn=1﹣2Sn , 又?jǐn)?shù)列{an}、{bn}滿足點(diǎn){an , 3 ![]() }在函數(shù)y=(
}在函數(shù)y=( ![]() )x的圖象上.
)x的圖象上.
(1)求數(shù)列{an},{bn}的通項(xiàng)公式;
(2)若cn=anbn+ ![]() ,求數(shù)列{an}的前n項(xiàng)和Tn .
,求數(shù)列{an}的前n項(xiàng)和Tn .
【答案】
(1)解:當(dāng)n≥2時,bn=1﹣2Sn,bn﹣1=1﹣2Sn﹣1,
兩式相減得:bn﹣bn﹣1=﹣2bn,即bn= ![]() bn﹣1,
bn﹣1,
又∵b1=1﹣2S1,即b1= ![]() ,
,
∴數(shù)列{bn}是首項(xiàng)、公比均為 ![]() 的等比數(shù)列,
的等比數(shù)列,
∴bn= ![]()
![]() =
= ![]() ;
;
∵點(diǎn){an,3 ![]() }在函數(shù)y=(
}在函數(shù)y=( ![]() )x的圖象上,
)x的圖象上,
∴3 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴數(shù)列{an}的通項(xiàng)公式an=2n﹣1
(2)解:由(1)可知cn=anbn+ ![]() =(2n﹣1)
=(2n﹣1) ![]() +3n,
+3n,
記數(shù)列{anbn}的前n項(xiàng)和為Pn,數(shù)列{ ![]() }的前n項(xiàng)和為Qn,
}的前n項(xiàng)和為Qn,
∵Pn=1 ![]() +3
+3 ![]() +…+(2n﹣1)
+…+(2n﹣1) ![]() ,
,
![]() Pn=1
Pn=1 ![]() +3
+3 ![]() +…+(2n﹣3)
+…+(2n﹣3) ![]() +(2n﹣1)
+(2n﹣1) ![]() ,
,
∴ ![]() Pn=
Pn= ![]() +2(
+2( ![]() +
+ ![]() +…+
+…+ ![]() )﹣(2n﹣1)
)﹣(2n﹣1) ![]()
= ![]() +2
+2 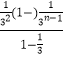 ﹣(2n﹣1)
﹣(2n﹣1) ![]()
= ![]() ﹣
﹣ ![]() ,
,
∴Pn=1﹣(n+1) ![]() ,
,
又∵Qn= ![]() =
= ![]() ,
,
∴Tn=Pn+Qn
=1﹣(n+1) ![]() +
+ ![]()
= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]()
【解析】(1)當(dāng)n≥2時,利用bn=1﹣2Sn與bn﹣1=1﹣2Sn﹣1作差,整理得bn= ![]() bn﹣1 , 進(jìn)而可知數(shù)列{bn}是首項(xiàng)、公比均為
bn﹣1 , 進(jìn)而可知數(shù)列{bn}是首項(xiàng)、公比均為 ![]() 的等比數(shù)列;通過將點(diǎn){an , 3
的等比數(shù)列;通過將點(diǎn){an , 3 ![]() }代入函數(shù)解析式y(tǒng)=(
}代入函數(shù)解析式y(tǒng)=( ![]() )x中,進(jìn)而計算可得結(jié)論;(2)通過(1)可知cn=(2n﹣1)
)x中,進(jìn)而計算可得結(jié)論;(2)通過(1)可知cn=(2n﹣1) ![]() +3n , 通過記數(shù)列{anbn}的前n項(xiàng)和為Pn , 數(shù)列{
+3n , 通過記數(shù)列{anbn}的前n項(xiàng)和為Pn , 數(shù)列{ ![]() }的前n項(xiàng)和為Qn , 利用錯位相減法計算可知Pn=1﹣(n+1)
}的前n項(xiàng)和為Qn , 利用錯位相減法計算可知Pn=1﹣(n+1) ![]() ,利用等比數(shù)列的求和公式計算可知Qn=
,利用等比數(shù)列的求和公式計算可知Qn= ![]() ,相加即得結(jié)論.
,相加即得結(jié)論.
【考點(diǎn)精析】本題主要考查了數(shù)列的前n項(xiàng)和和數(shù)列的通項(xiàng)公式的相關(guān)知識點(diǎn),需要掌握數(shù)列{an}的前n項(xiàng)和sn與通項(xiàng)an的關(guān)系 ;如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個公式表示,那么這個公式就叫這個數(shù)列的通項(xiàng)公式才能正確解答此題.
;如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個公式表示,那么這個公式就叫這個數(shù)列的通項(xiàng)公式才能正確解答此題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知偶函數(shù)f(x)和奇函數(shù)g(x)的定義域都是(﹣4,4),且在(﹣4,0]上的圖象如圖所示,則關(guān)于x的不等式f(x)g(x)<0的解集是 . 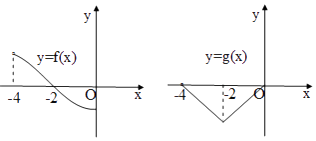
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】綜合題
(1)解不等式:3≤x2﹣2x<8;
(2)已知a,b,c,d均為實(shí)數(shù),求證:(a2+b2)(c2+d2)≥(ac+bd)2 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在區(qū)間D上,如果函數(shù)f(x)為減函數(shù),而xf(x)為增函數(shù),則稱f(x)為D上的弱減函數(shù).若f(x)= ![]()
(1)判斷f(x)在區(qū)間[0,+∞)上是否為弱減函數(shù);
(2)當(dāng)x∈[1,3]時,不等式 ![]() 恒成立,求實(shí)數(shù)a的取值范圍;
恒成立,求實(shí)數(shù)a的取值范圍;
(3)若函數(shù)g(x)=f(x)+k|x|﹣1在[0,3]上有兩個不同的零點(diǎn),求實(shí)數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,已知AA1=AB=AC,BC= ![]() AB,且AA1⊥平面ABC,點(diǎn)M、Q分別是BC、CC1的中點(diǎn),點(diǎn)P是棱A1B1上的任一點(diǎn).
AB,且AA1⊥平面ABC,點(diǎn)M、Q分別是BC、CC1的中點(diǎn),點(diǎn)P是棱A1B1上的任一點(diǎn). 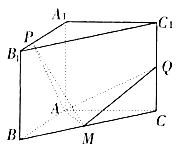
(1)求證:AQ⊥MP;
(2)若平面ACC1A1與平面AMP所成的銳角二面角為θ,且cosθ= ![]() ,試確定點(diǎn)P在棱A1B1上的位置,并說明理由.
,試確定點(diǎn)P在棱A1B1上的位置,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,a,b,c分別為角A,B,C所對的邊,角C是鈍角,且sinB= ![]() .
.
(1)求角C的值;
(2)若b=2,△ABC的面積為 ![]() ,求c的值.
,求c的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知以點(diǎn)C(t, ![]() )(t∈R且t≠0)為圓心的圓經(jīng)過原點(diǎn)O,且與x軸交于點(diǎn)A,與y軸交于點(diǎn)B.
)(t∈R且t≠0)為圓心的圓經(jīng)過原點(diǎn)O,且與x軸交于點(diǎn)A,與y軸交于點(diǎn)B.
(1)求證:△AOB的面積為定值.
(2)設(shè)直線2x+y﹣4=0與圓C交于點(diǎn)M,N,若|OM|=|ON|,求圓C的方程.
(3)在(2)的條件下,設(shè)P,Q分別是直線l:x+y+2=0和圓C上的動點(diǎn),求|PB|+|PQ|的最小值及此時點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系內(nèi),已知A(3,3)是⊙C上一點(diǎn),折疊該圓兩次使點(diǎn)A分別與圓上不相同的兩點(diǎn)(異于點(diǎn)A)重合,兩次的折痕方程分別為x﹣y+1=0和x+y﹣7=0,若⊙C上存在點(diǎn)P,使∠MPN=90°,其中M、N的坐標(biāo)分別為(﹣m,0)(m,0),則m的最大值為( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x2+4x+a﹣5,g(x)=m4x﹣1﹣2m+7.
(1)若函數(shù)f(x)在區(qū)間[﹣1,1]上存在零點(diǎn),求實(shí)數(shù)a的取值范圍;
(2)當(dāng)a=0時,若對任意的x1∈[1,2],總存在x2∈[1,2],使f(x1)=g(x2)成立,求實(shí)數(shù)m的取值范圍;
(3)若y=f(x)(x∈[t,2])的置于為區(qū)間D,是否存在常數(shù)t,使區(qū)間D的長度為6﹣4t?若存在,求出t的值;若不存在,請說明理由. (注:區(qū)間[p,q]的長度q﹣p)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com