
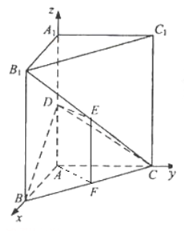
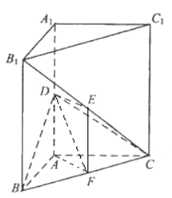
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.
(1)證明:![]() 平面
平面![]() ;
;
(2)已知![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見證明(2)![]()
【解析】
解法1:(1)建立空間直角坐標系,利用直線的向量和平面法向量平行證明線面垂直;
(2)設![]() ,利用
,利用![]() 與平面
與平面![]() 所成的角為
所成的角為![]() 得到
得到![]() 的值,再求出兩個面的法向量之間的夾角余弦值,得到二面角的余弦值.
的值,再求出兩個面的法向量之間的夾角余弦值,得到二面角的余弦值.
解法2:(1)取![]() 中點
中點![]() ,連接
,連接![]() 、
、![]() ,易證
,易證![]() 平面
平面![]() ,再證明
,再證明![]() ,可得
,可得![]() 平面
平面![]()
(2)設![]() ,利用
,利用![]() 與平面
與平面![]() 所成的角為
所成的角為![]() 得到
得到![]() 的值,再求出兩個面的法向量之間的夾角余弦值,得到二面角的余弦值.
的值,再求出兩個面的法向量之間的夾角余弦值,得到二面角的余弦值.
解法3:(1)同解法2
(2)設![]() ,利用三棱錐
,利用三棱錐![]() 等體積轉化,得到
等體積轉化,得到![]() 到面
到面![]() 的距離,利用
的距離,利用![]() 與平面
與平面![]() 所成的角為
所成的角為![]() 得到
得到![]() 與
與![]() 的關系,解出
的關系,解出![]() ,在兩個平面分別找出
,在兩個平面分別找出![]() 垂直于交線,得到二面角,求出其余弦值.
垂直于交線,得到二面角,求出其余弦值.
解法1:
(1)以![]() 為坐標原點,射線
為坐標原點,射線![]() 為
為![]() 軸的正半軸,建立如圖所示的直角坐標系
軸的正半軸,建立如圖所示的直角坐標系![]() .
.
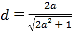
設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
因為![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]()
于是![]() 平面
平面![]() .
.
(2)設平面![]() 的法向量
的法向量![]() ,
,
則![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
故![]() ,取
,取![]() ,得
,得![]() .
.
因為![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,![]() ,
,
所以![]() ,
,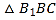
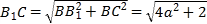 ,
,
解得![]() ,
,![]() .
.
由(1)知平面![]() 的法向量
的法向量![]() ,
,
 ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.
解法2:
(1)取![]() 中點
中點![]() ,連接
,連接![]() 、
、![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]()
![]() 平面
平面![]() .
.
![]() 為
為![]() 中點,
中點,![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() 四邊形
四邊形![]() 為平行四邊形,
為平行四邊形,
![]()
![]() .
.
![]()
![]() 平面
平面![]() .
.
(2)以![]() 為坐標原點,射線
為坐標原點,射線![]() 為
為![]() 軸的正半軸,建立如圖所示的直角坐標系
軸的正半軸,建立如圖所示的直角坐標系![]() .
.
設![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
設平面![]() 的法向量
的法向量![]() ,
,
則![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
故![]() ,
,
取![]() ,得
,得![]() .
.
因為![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,![]() ,
,
所以![]() ,
,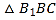
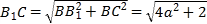 ,
,
解得![]() ,
,![]() .
.
由(1)知平面![]() 的法向量
的法向量![]() ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.
解法3:
(1)同解法2.
(2)設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() 到平面
到平面![]() 距離
距離![]() ,設
,設![]() 到面
到面![]() 距離為
距離為![]() ,
,
由![]()
得![]() ,即
,即![]()
![]() .
.
因為![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
所以![]() ,
,
而在直角三角形![]() 中
中![]() ,
,
所以![]() ,
,
解得![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 所以
所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 為二面角
為二面角![]() 的平面角,
的平面角,
而![]() ,可得四邊形
,可得四邊形![]() 是正方形,所以
是正方形,所以![]() ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
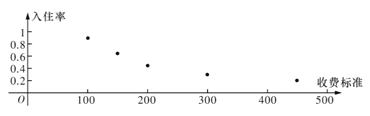
【題目】某創業者計劃在某旅游景區附近租賃一套農房發展成特色“農家樂”,為了確定未來發展方向此創業者對該景區附近五家“農家樂”跟蹤調查了100天,這五家“農家樂的收費標準互不相同得到的統計數據如下表,x為收費標準(單位:元/日),t為入住天數(單位:天),以頻率作為各自的“入住率”,收費標準x與“入住率”y的散點圖如圖
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
(1)若從以上五家“農家樂”中隨機抽取兩家深人調查,記![]() 為“入住率超過0.6的農家樂的個數,求
為“入住率超過0.6的農家樂的個數,求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散點圖判斷![]() 與
與![]() 哪個更合適于此模型(給出判斷即可不必說明理由)?并根據你的判斷結果求回歸方程(a,
哪個更合適于此模型(給出判斷即可不必說明理由)?并根據你的判斷結果求回歸方程(a,![]() 的結果精確到0.1)
的結果精確到0.1)
(3)根據第(2)問所求的回歸方程,試估計收費標準為多少時,100天銷售額L最大?(100天銷售額L=100×入住率×收費標準x)
參考數據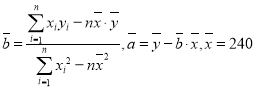 ,
,![]() ,
,![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為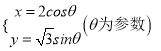 ,在同一平面直角坐標系中,將曲線
,在同一平面直角坐標系中,將曲線![]() 上的點按坐標變換
上的點按坐標變換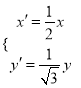 得到曲線
得到曲線![]() ,以原點為極點,
,以原點為極點, ![]() 軸的正半軸為極軸,建立極坐標系.
軸的正半軸為極軸,建立極坐標系.
(Ⅰ)求曲線![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)若過點![]() (極坐標)且傾斜角為
(極坐標)且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,弦
兩點,弦![]() 的中點為
的中點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程,下圖描述了甲、乙、丙三輛汽車在不同速度下的燃油效率情況. 下列敘述中正確的是( )

A. 消耗1升汽油,乙車最多可行駛5千米
B. 以相同速度行駛相同路程,三輛車中,甲車消耗汽油最多
C. 甲車以80千米/小時的速度行駛1小時,消耗10升汽油
D. 某城市機動車最高限速80千米/小時. 相同條件下,在該市用丙車比用乙車更省油
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次數學考試中,考生的成績號服從一個正態分布,即![]() .
.
(1)試求考試成績![]() 位于區間
位于區間![]() 上的概率是多少?
上的概率是多少?
(2)若這次考試共有2000名考生,試估計考試成績在![]() 的考生大約有多少人?
的考生大約有多少人?
(參考數據:![]() ;
;![]() ;
;![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的某種容器的體積為![]() ,它是由圓錐和圓柱兩部分連結而成的,圓柱與圓錐的底面圓半徑都為
,它是由圓錐和圓柱兩部分連結而成的,圓柱與圓錐的底面圓半徑都為![]() .圓錐的高為
.圓錐的高為![]() ,母線與底面所成的角為
,母線與底面所成的角為![]() ;圓柱的高為
;圓柱的高為![]() .已知圓柱底面造價為
.已知圓柱底面造價為![]() 元
元![]() ,圓柱側面造價為
,圓柱側面造價為![]() 元
元![]() ,圓錐側面造價為
,圓錐側面造價為![]() 元
元![]() .
.
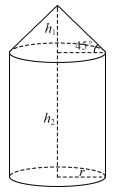
(1)將圓柱的高![]() 表示為底面圓半徑
表示為底面圓半徑![]() 的函數,并求出定義域;
的函數,并求出定義域;
(2)當容器造價最低時,圓柱的底面圓半徑![]() 為多少?
為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下命題中:
①若向量![]() 、
、![]() 、
、![]() 是空間的一組基底,則向量
是空間的一組基底,則向量![]() 、
、![]() 、
、![]() 也是空間的一組基底;
也是空間的一組基底;
②已知![]() 、
、![]() 、
、![]() 三點不共線,點
三點不共線,點![]() 為平面
為平面![]() 外任意一點,若點
外任意一點,若點![]() 滿足
滿足![]() ,則點
,則點![]() 平面
平面![]() ;
;
③曲線![]() 與曲線
與曲線![]() (
(![]() 且
且![]() )有相同的焦點.
)有相同的焦點.
④過定圓![]() 上一定點
上一定點![]() 作圓的動弦
作圓的動弦![]() ,
,![]() 為坐標原點,若
為坐標原點,若![]() ,則動點
,則動點![]() 的軌跡為橢圓;
的軌跡為橢圓;
⑤若過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于不同的兩點
于不同的兩點![]() ,且
,且![]() 是
是![]() 的中點,則直線
的中點,則直線![]() 的方程是
的方程是![]() .
.
其中真命題的序號是______.(寫出所有真命題的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com