
【題目】某市為增強市民的環(huán)境保護意識, 面向全市征召義務(wù)宣傳志愿者,現(xiàn)從符合條件的志愿者中隨機抽取![]() 名按年齡分組: 第
名按年齡分組: 第![]() 組
組![]() ,第2 組
,第2 組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示,
,得到的頻率分布直方圖如圖所示,
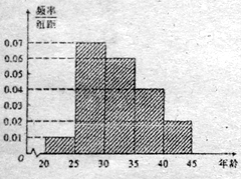
(1)若從第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 名志愿者參與廣場的宣傳活動, 應(yīng)從第
名志愿者參與廣場的宣傳活動, 應(yīng)從第![]() 組各抽取多少名志愿者?
組各抽取多少名志愿者?
(2)在(1)的條件下, 該縣決定在這![]() 名志愿者中隨機抽取
名志愿者中隨機抽取![]() 名志愿者介紹宣傳經(jīng)驗, 求第
名志愿者介紹宣傳經(jīng)驗, 求第![]() 組至少有—名志愿者被抽中的概率.
組至少有—名志愿者被抽中的概率.
【答案】(1)![]() 人,
人,![]() 人,
人,![]() 人;(2)
人;(2)![]() .
.
【解析】
試題分析:(1)通過計算頻率可得:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ;(2)結(jié)合樹狀圖可以列舉從
;(2)結(jié)合樹狀圖可以列舉從![]() 名志愿者中抽取
名志愿者中抽取![]() 名志愿者共
名志愿者共![]() 種基本事件,其中至少有一名志愿者被抽中的有
種基本事件,其中至少有一名志愿者被抽中的有![]() 種基本事件,從而第
種基本事件,從而第![]() 組至少有一名志愿者被抽中的概率
組至少有一名志愿者被抽中的概率![]() .
.
試題解析:(1)第![]() 組的人數(shù)為
組的人數(shù)為![]() , 第
, 第![]() 組的人數(shù)為
組的人數(shù)為![]() ,第
,第![]() 組的人數(shù)為
組的人數(shù)為![]() ,因為第
,因為第![]() 組共有
組共有![]() 名志愿者, 所以利用分層抽樣的方法在
名志愿者, 所以利用分層抽樣的方法在![]() 名志愿者中抽取
名志愿者中抽取![]() 名志愿者, 每組抽取的人數(shù)分別為: 第
名志愿者, 每組抽取的人數(shù)分別為: 第![]() 組
組![]() ;第
;第![]() 組
組![]() ;第
;第![]() 組
組![]() .所以應(yīng)從第
.所以應(yīng)從第![]() 組中分別抽取
組中分別抽取![]() 人,
人,![]() 人,
人,![]() 人.
人.
(2)記第![]() 組
組![]() 名志愿者為
名志愿者為![]() ,第
,第![]() 組
組![]() 名志愿者為
名志愿者為![]() 第
第![]() 組
組![]() 名志愿者為
名志愿者為![]() ,則從
,則從![]() 名志愿者中抽取
名志愿者中抽取![]() 名志愿者有:
名志愿者有:![]()
![]() ,共
,共![]() 種.
種.
其中第![]() 組的
組的![]() 名志愿者為
名志愿者為![]() 至少有一名志愿者被抽中的有:
至少有一名志愿者被抽中的有:
![]() ,
,![]() 共
共![]() 種.
種.
所以第![]() 組至少有一名志愿者被抽中的概率
組至少有一名志愿者被抽中的概率![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間和極值;
的單調(diào)區(qū)間和極值;
(2)證明:當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 沒有零點(提示:
沒有零點(提示:![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(Ⅰ)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最值;
上的最值;
(Ⅱ)當(dāng)![]() 時,設(shè)函數(shù)
時,設(shè)函數(shù)![]() (其中
(其中![]() 為常數(shù))的3個極值點為
為常數(shù))的3個極值點為![]() ,且
,且![]() ,將
,將![]() 這5個數(shù)按照從小到大的順序排列,并證明你的結(jié)論.
這5個數(shù)按照從小到大的順序排列,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)生產(chǎn)甲乙兩種產(chǎn)品均需用A,B兩種原料,已知生產(chǎn)1噸每種產(chǎn)品需原料及每天原料的可用限額如右表所示,如果生產(chǎn)1噸甲、乙產(chǎn)品可獲利潤分別為3萬元、4萬元,則該企業(yè)每天可獲得最大利潤為( )
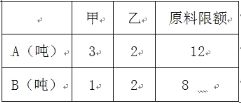
A.12萬元 B.16萬元
C.17萬元 D.18萬元
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知方程![]() .
.
(1)求該方程表示一條直線的條件;
(2)當(dāng)![]() 為何實數(shù)時,方程表示的直線斜率不存在?求出這時的直線方程;
為何實數(shù)時,方程表示的直線斜率不存在?求出這時的直線方程;
(3)已知方程表示的直線![]() 在
在![]() 軸上的截距為-3,求實數(shù)
軸上的截距為-3,求實數(shù)![]() 的值;
的值;
(4)若方程表示的直線![]() 的傾斜角是45°,求實數(shù)
的傾斜角是45°,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程,在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為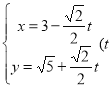 為參數(shù)),在極坐標(biāo)系(與直角坐標(biāo)系
為參數(shù)),在極坐標(biāo)系(與直角坐標(biāo)系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極軸,以
為極軸,以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的方程為
的方程為![]() .
.
(1)求圓![]() 的圓心到直線
的圓心到直線![]() 的距離;
的距離;
(2)設(shè)圓![]() 與直線
與直線![]() 交于點
交于點![]() ,若點
,若點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,求
,求![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com