
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間和極值;
的單調區間和極值;
(2)證明:當![]() 時,函數
時,函數![]() 沒有零點(提示:
沒有零點(提示:![]() ).
).
【答案】(1)單調增區間為![]() ,單調減區間為
,單調減區間為![]() ,極小值為
,極小值為![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
試題分析:(1)對函數![]() 進行化簡求導得
進行化簡求導得![]() .利用導數工具可得:當
.利用導數工具可得:當![]() 時,
時,![]() 取得極小值
取得極小值![]() ;(2)由(1)可知
;(2)由(1)可知![]() 取得極小值,亦即最小值為:
取得極小值,亦即最小值為:
![]() ,又
,又![]()
![]()
![]() ,設
,設![]()
![]() ,利用導數工具得
,利用導數工具得![]() 有唯一的零點
有唯一的零點![]() ,使得
,使得![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.又由于
上單調遞減.又由于![]()
![]()
![]() 恒成立
恒成立![]()
![]() 恒成立
恒成立![]()
![]() 恒成立
恒成立![]() 當
當![]() 時,函數
時,函數![]() 沒有零點.
沒有零點.
試題解析:(1)因為![]() ,
,
所以![]() .
.
因為![]() ,所以當
,所以當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() .
.
所以函數![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .
.
當![]() 時,
時,![]() 取得極小值
取得極小值![]() .
.
(2)由(1)可知:當![]() 時,
時,![]() 取得極小值,亦即最小值.
取得極小值,亦即最小值.
![]() ,又因為
,又因為![]() ,所以
,所以![]() ,
,
設![]()
![]() ,則
,則![]() .
.
因為![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,
,
所以![]() 有唯一的零點
有唯一的零點![]() ,使得
,使得![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
又由于![]() .
.
所以![]() 恒成立,從而
恒成立,從而![]() 恒成立,則
恒成立,則![]() 恒成立.
恒成立.
所以當![]() 時,函數
時,函數![]() 沒有零點.
沒有零點.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:高中數學 來源: 題型:
【題目】在互聯網時代,網校培訓已經成為青年學習的一種趨勢,假設某網校的套題每日的銷售量![]() (單位:千套)與銷售價格
(單位:千套)與銷售價格![]() (單位:元/套)滿足的關系式
(單位:元/套)滿足的關系式![]() (
(![]() ,
,![]() 為常數),其中
為常數),其中![]() 與
與![]() 成反比,
成反比,![]() 與
與![]() 的平方成正比,已知銷售價格為5元/套時,每日可售出套題21千套,銷售價格為3.5元/套時,每日可售出套題69千套.
的平方成正比,已知銷售價格為5元/套時,每日可售出套題21千套,銷售價格為3.5元/套時,每日可售出套題69千套.
(1) 求![]() 的表達式;
的表達式;
(2) 假設網校的員工工資,辦公等所有開銷折合為每套題3元(只考慮銷售出的套數),試確定銷售價格![]() 的值,使網校每日銷售套題所獲得的利潤最大.(保留1位小數)
的值,使網校每日銷售套題所獲得的利潤最大.(保留1位小數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點E為正方形ABCD邊CD上異于點C,D的動點,將△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,則下列說法中正確的有( )
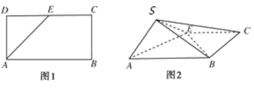
①存在點E使得直線SA⊥平面SBC;
②平面SBC內存在直線與SA平行
③平面ABCE內存在直線與平面SAE平行;
④存在點E使得SE⊥BA.
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業共有20條生產線,由于受生產能力和技術水平等因素的影響,會產生一定量的次品.根據經驗知道,每臺機器產生的次品數![]() 萬件與每臺機器的日產量
萬件與每臺機器的日產量![]() 萬件
萬件![]() 之間滿足關系:
之間滿足關系: ![]() .已知每生產1萬件合格的產品可以以盈利3萬元,但每生產1萬件次品將虧損1萬元.
.已知每生產1萬件合格的產品可以以盈利3萬元,但每生產1萬件次品將虧損1萬元.
(Ⅰ)試將該企業每天生產這種產品所獲得的利潤![]() 表示為
表示為![]() 的函數;
的函數;
(Ⅱ)當每臺機器的日產量為多少時,該企業的利潤最大,最大為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分別為角A,B,C的對邊,在四面體PABC中,S1,S2,S3,S分別表示△PAB,△PBC,△PCA,△ABC的面積,α,β,γ依次表示面PAB,面PBC,面PCA與底面ABC所成二面角的大小.寫出對四面體性質的猜想,并證明你的結論


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業共有20條生產線,由于受生產能力和技術水平等因素的影響,會產生一定量的次品.根據經驗知道,每臺機器產生的次品數![]() 萬件與每臺機器的日產量
萬件與每臺機器的日產量![]() 萬件
萬件![]() 之間滿足關系:
之間滿足關系:![]() .已知每生產1萬件合格的產品可以以盈利3萬元,但每生產1萬件次品將虧損1萬元.
.已知每生產1萬件合格的產品可以以盈利3萬元,但每生產1萬件次品將虧損1萬元.
(Ⅰ)試將該企業每天生產這種產品所獲得的利潤![]() 表示為
表示為![]() 的函數;
的函數;
(Ⅱ)當每臺機器的日產量為多少時,該企業的利潤最大,最大為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為增強市民的環境保護意識, 面向全市征召義務宣傳志愿者,現從符合條件的志愿者中隨機抽取![]() 名按年齡分組: 第
名按年齡分組: 第![]() 組
組![]() ,第2 組
,第2 組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示,
,得到的頻率分布直方圖如圖所示,
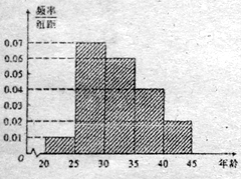
(1)若從第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 名志愿者參與廣場的宣傳活動, 應從第
名志愿者參與廣場的宣傳活動, 應從第![]() 組各抽取多少名志愿者?
組各抽取多少名志愿者?
(2)在(1)的條件下, 該縣決定在這![]() 名志愿者中隨機抽取
名志愿者中隨機抽取![]() 名志愿者介紹宣傳經驗, 求第
名志愿者介紹宣傳經驗, 求第![]() 組至少有—名志愿者被抽中的概率.
組至少有—名志愿者被抽中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com