【題目】矩形ABCD中，
，沿對角線AC將三角形ADC折起，得到四面體
，四面體 外接球表面積為
，當四面體的體積取最大值時，四面體的表面積為（ ）
A.
B.
C.
D.
科目：高中數學 來源： 題型：
【題目】已知拋物線C：y2=4x的焦點為F，過點F且斜率為1的直線與拋物線C交于A、B兩點，若在以線段AB為直徑的圓上存在兩點M、N，在直線
：x+y+a=0上存在一點Q，使得∠MQN=90°，則實數a的取值范圍為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平行四邊形ABCD中，AB=1，AD
，且∠BAD=45°，以BD為折線，把△ABD折起，使AB⊥DC，連接AC，得到三棱錐A﹣BCD.
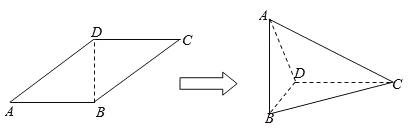
(1)求證：平面ABD⊥平面BCD；
(2)求二面角B﹣AC﹣D的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知銳角△ABC中，角A，B，C的對邊分別為a，b，c，b+c=10，a=
，5bsinAcosC+5csinAcosB=3a．
（1）求A的余弦值；
（2）求b和c．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】據報道，全國很多省市將英語考試作為高考改革的重點，一時間“英語考試該如何改革”引起廣泛關注，為了解某地區學生和包括老師、家長在內的社會人士對高考英語改革的看法，某媒體在該地區選擇了3 000人進行調查，就“是否取消英語聽力”問題進行了問卷調查統計，結果如下表：
態度 | |||
調查人群 | 應該取消 | 應該保留 | 無所謂 |
在校學生 | 2100人 | 120人 | y人 |
社會人士 | 500人 | x人 | z人 |
已知在全體樣本中隨機抽取1人，抽到持“應該保留”態度的人的概率為0.06.
(1)現用分層抽樣的方法在所有參與調查的人中抽取300人進行問卷訪談，問應在持“無所謂”態度的人中抽取多少人？
(2)在持“應該保留”態度的人中，用分層抽樣的方法抽取6人，然后從這6人中隨機抽取2人，求這2人中恰好有1個人為在校學生的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正實數列a1，a2，…滿足對于每個正整數k，均有
，證明：
（Ⅰ）a1+a2≥2；
（Ⅱ）對于每個正整數n≥2，均有a1+a2+…+an≥n．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“工資條里顯紅利，個稅新政入民心”.隨著2019年新年鐘聲的敲響，我國自1980年以來，力度最大的一次個人所得稅（簡稱個稅）改革迎來了全面實施的階段.某
從業者為了解自己在個稅新政下能享受多少稅收紅利，繪制了他在26歲-35歲（2009年-2018年）之間各年的月平均收入
（單位：千元）的散點圖：(注：年齡代碼1-10分別對應年齡26-35歲)
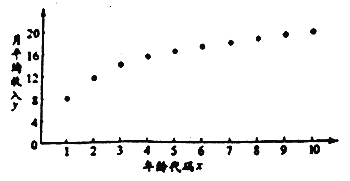
（1）由散點圖知，可用回歸模型
擬合與
的關系，試根據有關數據建立關于的回歸方程；
（2）如果該從業者在個稅新政下的專項附加扣除為3000元/月，試利用（1）的結果，將月平均收入視為月收入，根據新舊個稅政策，估計他36歲時每個月少繳納的個人所得稅.
附注：①參考數據：
，
，
，
，
，
，
，其中
：取
，
.
②參考公式：回歸方程
中斜率和截距的最小二乘估計分別為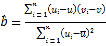
，
.
③新舊個稅政策下每月應納稅所得額（含稅）計算方法及稅率表如下：
舊個稅稅率表（個稅起征點3500元） | 新個稅稅率表（個稅起征點5000元） | |||
繳稅 級數 | 每月應納稅所得額（含稅） | 稅率 | 每月應納稅所得額（含稅） | 稅率 |
1 | 不超過1500元的都分 | 3 | 不超過3000元的都分 | 3 |
2 | 超過1500元至4500元的部分 | 10 | 超過3000元至12000元的部分 | 10 |
3 | 超過4500元至9000元的部分 | 20 | 超過12000元至25000元的部分 | 20 |
4 | 超過9000元至35000元的部分 | 25 | 超過25000元至35000元的部分 | 25 |
5 | 超過35000元至55000元的部分 | 30 | 超過35000元至55000元的部分 | 30 |
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
