
【題目】小張?jiān)谔詫毦W(wǎng)上開(kāi)一家商店,他以10元每條的價(jià)格購(gòu)進(jìn)某品牌積壓圍巾2000條.定價(jià)前,小張先搜索了淘寶網(wǎng)上的其它網(wǎng)店,發(fā)現(xiàn):A商店以30元每條的價(jià)格銷(xiāo)售,平均每日銷(xiāo)售量為10條;B商店以25元每條的價(jià)格銷(xiāo)售,平均每日銷(xiāo)售量為20條.假定這種圍巾的銷(xiāo)售量t(條)是售價(jià)x(元)(x∈Z+)的一次函數(shù),且各個(gè)商店間的售價(jià)、銷(xiāo)售量等方面不會(huì)互相影響.
(1)試寫(xiě)出圍巾銷(xiāo)售每日的毛利潤(rùn)y(元)關(guān)于售價(jià)x(元)(x∈Z+)的函數(shù)關(guān)系式(不必寫(xiě)出定義域),并幫助小張定價(jià),使得每日的毛利潤(rùn)最高(每日的毛利潤(rùn)為每日賣(mài)出商品的進(jìn)貨價(jià)與銷(xiāo)售價(jià)之間的差價(jià));
(2)考慮到這批圍巾的管理、倉(cāng)儲(chǔ)等費(fèi)用為200元/天(只要圍巾沒(méi)有售完,均須支付200元/天,管理、倉(cāng)儲(chǔ)等費(fèi)用與圍巾數(shù)量無(wú)關(guān)),試問(wèn)小張應(yīng)該如何定價(jià),使這批圍巾的總利潤(rùn)最高(總利潤(rùn)=總毛利潤(rùn)﹣總管理、倉(cāng)儲(chǔ)等費(fèi)用)?
【答案】
(1)解:設(shè)t=kx+b,∴ ![]() ,解得k=﹣2,b=70,∴t=70﹣2x.
,解得k=﹣2,b=70,∴t=70﹣2x.
y=(x﹣10)t=(x﹣10)(70﹣2x)=﹣2x2+90x﹣700,
∵ ![]() ,∴圍巾定價(jià)為22元或23元時(shí),每日的利潤(rùn)最高
,∴圍巾定價(jià)為22元或23元時(shí),每日的利潤(rùn)最高
(2)解:設(shè)售價(jià)x(元)時(shí)總利潤(rùn)為z(元),
∴z=2000(x﹣10)﹣200 ![]()
=2000(25﹣((35﹣x)+ ![]() ))≤2000(25﹣
))≤2000(25﹣ ![]() )=10000元.
)=10000元.
當(dāng)35﹣x= ![]() 時(shí),即x=25時(shí),取得等號(hào).
時(shí),即x=25時(shí),取得等號(hào).
∴小張的這批圍巾定價(jià)為25元時(shí),這批圍巾的總利潤(rùn)最高
【解析】(1)根據(jù)題意先求出銷(xiāo)售量t與售價(jià)x之間的關(guān)系式,再利用毛利潤(rùn)為每日賣(mài)出商品的進(jìn)貨價(jià)與銷(xiāo)售價(jià)之間的差價(jià),確定毛利潤(rùn)y(元)關(guān)于售價(jià)x(元)(x∈Z+)的函數(shù)關(guān)系式,利用二次函數(shù)求最值的方法可求;(2)根據(jù)總利潤(rùn)=總毛利潤(rùn)﹣總管理、倉(cāng)儲(chǔ)等費(fèi)用,構(gòu)建函數(shù)關(guān)系,利用基本不等式可求最值.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 為梯形,
為梯形, ![]() ,且
,且![]() 與
與![]() 均為正三角形,
均為正三角形, ![]() 為
為![]() 的重心.
的重心.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的正切值.
所成銳二面角的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() :
: ![]() 的上下頂點(diǎn)分別為
的上下頂點(diǎn)分別為![]() ,且點(diǎn)
,且點(diǎn)![]() .
. ![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點(diǎn),且
的左、右焦點(diǎn),且![]() .
.
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)點(diǎn)![]() 是橢圓上異于
是橢圓上異于![]() ,
, ![]() 的任意一點(diǎn),過(guò)點(diǎn)
的任意一點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 軸于
軸于![]() ,
, ![]() 為線段
為線段![]()
的中點(diǎn).直線![]() 與直線
與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,
, ![]() 為線段
為線段![]() 的中點(diǎn),
的中點(diǎn), ![]() 為坐標(biāo)原點(diǎn).求
為坐標(biāo)原點(diǎn).求
![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() ,若存在常數(shù)
,若存在常數(shù)![]() ,使得對(duì)任意
,使得對(duì)任意![]() ,均有
,均有![]() ,則稱(chēng)
,則稱(chēng)![]() 為有界集合,同時(shí)稱(chēng)
為有界集合,同時(shí)稱(chēng)![]() 為集合
為集合![]() 的上界.
的上界.
(1)設(shè)![]() 、
、![]() ,試判斷
,試判斷![]() 、
、![]() 是否為有界集合,并說(shuō)明理由;
是否為有界集合,并說(shuō)明理由;
(2)已知![]() ,記
,記![]() (
(![]() ).若
).若![]() ,
,
![]() ,且
,且![]() 為有界集合,求
為有界集合,求![]() 的值及
的值及![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() 均為正數(shù),將
均為正數(shù),將![]() 中的最小數(shù)記為
中的最小數(shù)記為![]() .是否存在正數(shù)
.是否存在正數(shù)![]() ,使得
,使得![]() 為有界集合
為有界集合![]() ,
, ![]() 均為正數(shù)
均為正數(shù)![]() 的上界,若存在,試求
的上界,若存在,試求![]() 的最小值;若不存在,請(qǐng)說(shuō)明理由.
的最小值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù) ![]() 的值域?yàn)榧螦,關(guān)于x的不等式
的值域?yàn)榧螦,關(guān)于x的不等式 ![]() 的解集為B,集合
的解集為B,集合 ![]() ,集合D={x|m+1≤x<2m﹣1}(m>0)
,集合D={x|m+1≤x<2m﹣1}(m>0)
(1)若A∪B=B,求實(shí)數(shù)a的取值范圍;
(2)若DC,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)y=f(x),若在定義域內(nèi)存在x0 , 使得f(﹣x0)=﹣f(x0)成立,則稱(chēng)x0為函數(shù)y=f(x)的局部對(duì)稱(chēng)點(diǎn).
(1)若a、b∈R且a≠0,證明:函數(shù)f(x)=ax2+bx﹣a必有局部對(duì)稱(chēng)點(diǎn);
(2)若函數(shù)f(x)=2x+c在定義域[﹣1,2]內(nèi)有局部對(duì)稱(chēng)點(diǎn),求實(shí)數(shù)c的取值范圍;
(3)若函數(shù)f(x)=4x﹣m2x+1+m2﹣3在R上有局部對(duì)稱(chēng)點(diǎn),求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在直四棱柱ABCD-A1B1C1D1中,底面四邊形ABCD為菱形,A1A=AB=2,∠ABC=![]() ,E,F分別是BC,A1C的中點(diǎn).
,E,F分別是BC,A1C的中點(diǎn).
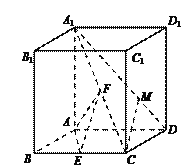
(1)求異面直線EF,AD所成角的余弦值;
(2)點(diǎn)M在線段A1D上, ![]() .若CM∥平面AEF,求實(shí)數(shù)λ的值.
.若CM∥平面AEF,求實(shí)數(shù)λ的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (
(![]() )與函數(shù)
)與函數(shù)![]() 有公共切線.
有公共切線.
(Ⅰ)求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若不等式![]() 對(duì)于
對(duì)于![]() 的一切值恒成立,求
的一切值恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com