Question

【題目】已知函數f（x）=|x+1|﹣|x﹣2|．
（Ⅰ）求不等式f（x）≥1的解集；
（Ⅱ）若不等式f（x）≥x2﹣x+m的解集非空，求m的取值范圍．

Answer 1

【答案】解：（Ⅰ）∵f（x）=|x+1|﹣|x﹣2|= 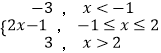，f（x）≥1，
∴當﹣1≤x≤2時，2x﹣1≥1，解得1≤x≤2；
當x＞2時，3≥1恒成立，故x＞2；
綜上，不等式f（x）≥1的解集為{x|x≥1}．
（Ⅱ）原式等價于存在x∈R使得f（x）﹣x2+x≥m成立，
即m≤[f（x）﹣x2+x]max ， 設g（x）=f（x）﹣x2+x．
由（1）知，g（x）= ，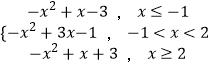
當x≤﹣1時，g（x）=﹣x2+x﹣3，其開口向下，對稱軸方程為x= ＞﹣1，
∴g（x）≤g（﹣1）=﹣1﹣1﹣3=﹣5；
當﹣1＜x＜2時，g（x）=﹣x2+3x﹣1，其開口向下，對稱軸方程為x= ∈（﹣1，2），
∴g（x）≤g（ ）=﹣ + ﹣1= ；
當x≥2時，g（x）=﹣x2+x+3，其開口向下，對稱軸方程為x= ＜2，
∴g（x）≤g（2）=﹣4+2=3=1；
綜上，g（x）max= ，
∴m的取值范圍為（﹣∞， ]．
【解析】（Ⅰ）由于f（x）=|x+1|﹣|x﹣2|= 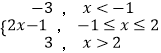，解不等式f（x）≥1可分﹣1≤x≤2與x＞2兩類討論即可解得不等式f（x）≥1的解集；
（Ⅱ）依題意可得m≤[f（x）﹣x2+x]max ， 設g（x）=f（x）﹣x2+x，分x≤1、﹣1＜x＜2、x≥2三類討論，可求得g（x）max= ，從而可得m的取值范圍．
【考點精析】解答此題的關鍵在于理解函數的值域的相關知識，掌握求函數值域的方法和求函數最值的常用方法基本上是相同的．事實上，如果在函數的值域中存在一個最小（大）數，這個數就是函數的最小（大）值．因此求函數的最值與值域，其實質是相同的，以及對絕對值不等式的解法的理解，了解含絕對值不等式的解法：定義法、平方法、同解變形法，其同解定理有；規律：關鍵是去掉絕對值的符號．