
【題目】已知![]() 是等差數(shù)列,其前
是等差數(shù)列,其前![]() 項中的奇數(shù)項的和與偶數(shù)項的和之差為
項中的奇數(shù)項的和與偶數(shù)項的和之差為![]() .
.
(1)請證明這一結(jié)論對任意等差數(shù)列![]() (
(![]() 中各項均不為零)恒成立;
中各項均不為零)恒成立;
(2)請類比等差數(shù)列的結(jié)論,對于各項均為正數(shù)的等比數(shù)列![]() ,提出猜想,并加以證明.
,提出猜想,并加以證明.
【答案】(1)證明見解析(2)類比猜想:各項均為正數(shù)的等比數(shù)列![]() 的前
的前![]() 項中奇數(shù)項的積與偶數(shù)項的積的比為
項中奇數(shù)項的積與偶數(shù)項的積的比為![]() ,證明見解析
,證明見解析
【解析】
(1)由![]() ,
,![]() 可得
可得![]()
(2)類比猜想可得:各項均為正數(shù)的等比數(shù)列![]() 的前
的前![]() 項中奇數(shù)項的積與偶數(shù)項的積的比為
項中奇數(shù)項的積與偶數(shù)項的積的比為![]() ,然后證明出來即可.
,然后證明出來即可.
證明:(1)記![]() 為等差數(shù)列
為等差數(shù)列![]() 前
前![]() 項中奇數(shù)項的和,
項中奇數(shù)項的和,
![]() 為等差數(shù)列
為等差數(shù)列![]() 前
前![]() 項中偶數(shù)項的和,
項中偶數(shù)項的和,
由等差數(shù)列的前![]() 項和公式可得
項和公式可得![]() ,
,
![]() ,
,
![]() .
.
![]() 命題成立.
命題成立.
(2)解:類比猜想可得:各項均為正數(shù)的等比數(shù)列![]() 的前
的前![]() 項中奇數(shù)項的積與偶數(shù)項的積的比為
項中奇數(shù)項的積與偶數(shù)項的積的比為![]() .
.
證明:記各項均為正數(shù)的等比數(shù)列![]() 的前
的前![]() 項中奇數(shù)項的積為
項中奇數(shù)項的積為![]() ,
,
偶數(shù)項的積為![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,
,
 ,即
,即![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】某省積極響應教育部號召實行新課程改革,為了調(diào)查某校高三學生的物理考試成績是否達到![]() 級與學生性別是否有關(guān),從該校高三學生中隨機抽取了部分男女生的成績得到如下列聯(lián)表:
級與學生性別是否有關(guān),從該校高三學生中隨機抽取了部分男女生的成績得到如下列聯(lián)表:
考試成績達到 | 考試成績未達到 | 總計 | |
男生 | 26 | 40 | |
女生 | 6 | ||
總計 | 70 |
(1)(ⅰ)將![]() 列聯(lián)表補充完整;
列聯(lián)表補充完整;
(ⅱ)據(jù)此列聯(lián)表判斷,能否有![]() 的把握認為“物理考試成績是否達到級與性別有關(guān)”?
的把握認為“物理考試成績是否達到級與性別有關(guān)”?
(2)將頻率視作概率,從該校高三年級任意抽取3名學生的成績,求物理考試成績達到![]() 級的人數(shù)的分布列及期望.
級的人數(shù)的分布列及期望.
附: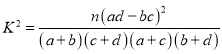
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10..828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校開設(shè)了射擊選修課,規(guī)定向![]() 、
、![]() 兩個靶進行射擊:先向
兩個靶進行射擊:先向![]() 靶射擊一次,命中得1分,沒有命中得0分,向
靶射擊一次,命中得1分,沒有命中得0分,向![]() 靶連續(xù)射擊兩次,每命中一次得2分,沒命中得0分;小明同學經(jīng)訓練可知:向
靶連續(xù)射擊兩次,每命中一次得2分,沒命中得0分;小明同學經(jīng)訓練可知:向![]() 靶射擊,命中的概率為
靶射擊,命中的概率為![]() ,向
,向![]() 靶射擊,命中的概率為
靶射擊,命中的概率為![]() ,假設(shè)小明同學每次射擊的結(jié)果相互獨立.現(xiàn)對小明同學進行以上三次射擊的考核.
,假設(shè)小明同學每次射擊的結(jié)果相互獨立.現(xiàn)對小明同學進行以上三次射擊的考核.
(1)求小明同學恰好命中一次的概率;
(2)求小明同學獲得總分![]() 的分布列及數(shù)學期望
的分布列及數(shù)學期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列關(guān)于獨立性檢驗的敘述
①常用等高條形圖表示列聯(lián)表數(shù)據(jù)的頻率特征;
②獨立性檢驗依據(jù)小概率原理;
③獨立性檢驗的結(jié)果是完全正確的;
④對分類變量![]() 與
與![]() 的隨機變量
的隨機變量![]() 的觀測值
的觀測值![]() 來說,
來說,![]() 越小,
越小,![]() 與
與![]() 有關(guān)系的把握程度就越大.
有關(guān)系的把握程度就越大.
其中敘述正確的個數(shù)為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】有如下命題,其中真命題的標號為( )
A.若冪函數(shù)![]() 的圖象過點
的圖象過點![]() ,則
,則![]()
B.函數(shù)![]() (
(![]() ,且
,且![]() )的圖象恒過定點
)的圖象恒過定點![]()
C.函數(shù)![]() 有兩個零點
有兩個零點
D.若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為4,最小值為3,則實數(shù)m的取值范圍是
上的最大值為4,最小值為3,則實數(shù)m的取值范圍是![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)集合![]() ,
,![]() 是非空集合
是非空集合![]() 的兩個不同子集.
的兩個不同子集.
(1)若![]() ,且
,且![]() 是
是![]() 的子集,求所有有序集合對
的子集,求所有有序集合對![]() 的個數(shù);
的個數(shù);
(2)若![]() ,且
,且![]() 是
是![]() 的子集,求所有有序集合對
的子集,求所有有序集合對![]() 的個數(shù).
的個數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某屆奧運會上,中國隊以26金18銀26銅的成績稱金牌榜第三、獎牌榜第二,某校體育愛好者在高三年級一班至六班進行了“本屆奧運會中國隊表現(xiàn)”的滿意度調(diào)查![]() 結(jié)果只有“滿意”和“不滿意”兩種
結(jié)果只有“滿意”和“不滿意”兩種![]() ,從被調(diào)查的學生中隨機抽取了50人,具體的調(diào)查結(jié)果如表:
,從被調(diào)查的學生中隨機抽取了50人,具體的調(diào)查結(jié)果如表:
班號 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
頻數(shù) | 5 | 9 | 11 | 9 | 7 | 9 |
滿意人數(shù) | 4 | 7 | 8 | 5 | 6 | 6 |
(1)在高三年級全體學生中隨機抽取一名學生,由以上統(tǒng)計數(shù)據(jù)估計該生持滿意態(tài)度的概率;
(2)若從一班至二班的調(diào)查對象中隨機選取4人進行追蹤調(diào)查,記選中的4人中對“本屆奧運會中國隊表現(xiàn)”不滿意的人數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為檢驗![]() 兩條生產(chǎn)線的優(yōu)品率,現(xiàn)從兩條生產(chǎn)線上各抽取
兩條生產(chǎn)線的優(yōu)品率,現(xiàn)從兩條生產(chǎn)線上各抽取![]() 件產(chǎn)品進行檢測評分,用莖葉圖的形式記錄,并規(guī)定高于
件產(chǎn)品進行檢測評分,用莖葉圖的形式記錄,并規(guī)定高于![]() 分為優(yōu)品.前
分為優(yōu)品.前![]() 件的評分記錄如下,第
件的評分記錄如下,第![]() 件暫不公布.
件暫不公布.

(1)求所抽取的![]() 生產(chǎn)線上的
生產(chǎn)線上的![]() 個產(chǎn)品的總分小于
個產(chǎn)品的總分小于![]() 生產(chǎn)線上的第
生產(chǎn)線上的第![]() 個產(chǎn)品的總分的概率;
個產(chǎn)品的總分的概率;
(2)已知![]() 生產(chǎn)線的第
生產(chǎn)線的第![]() 件產(chǎn)品的評分分別為
件產(chǎn)品的評分分別為![]() .
.
①從![]() 生產(chǎn)線的
生產(chǎn)線的![]() 件產(chǎn)品里面隨機抽取
件產(chǎn)品里面隨機抽取![]() 件,設(shè)非優(yōu)品的件數(shù)為
件,設(shè)非優(yōu)品的件數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學期望;
的分布列和數(shù)學期望;
②以所抽取的樣本優(yōu)品率來估計![]() 生產(chǎn)線的優(yōu)品率,從
生產(chǎn)線的優(yōu)品率,從![]() 生產(chǎn)線上隨機抽取
生產(chǎn)線上隨機抽取![]() 件產(chǎn)品,記優(yōu)品的件數(shù)為
件產(chǎn)品,記優(yōu)品的件數(shù)為![]() ,求
,求![]() 的數(shù)學期望.
的數(shù)學期望.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com