
【題目】某省積極響應(yīng)教育部號召實行新課程改革,為了調(diào)查某校高三學(xué)生的物理考試成績是否達(dá)到![]() 級與學(xué)生性別是否有關(guān),從該校高三學(xué)生中隨機(jī)抽取了部分男女生的成績得到如下列聯(lián)表:
級與學(xué)生性別是否有關(guān),從該校高三學(xué)生中隨機(jī)抽取了部分男女生的成績得到如下列聯(lián)表:
考試成績達(dá)到 | 考試成績未達(dá)到 | 總計 | |
男生 | 26 | 40 | |
女生 | 6 | ||
總計 | 70 |
(1)(ⅰ)將![]() 列聯(lián)表補(bǔ)充完整;
列聯(lián)表補(bǔ)充完整;
(ⅱ)據(jù)此列聯(lián)表判斷,能否有![]() 的把握認(rèn)為“物理考試成績是否達(dá)到級與性別有關(guān)”?
的把握認(rèn)為“物理考試成績是否達(dá)到級與性別有關(guān)”?
(2)將頻率視作概率,從該校高三年級任意抽取3名學(xué)生的成績,求物理考試成績達(dá)到![]() 級的人數(shù)的分布列及期望.
級的人數(shù)的分布列及期望.
附: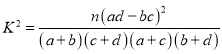
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10..828 |
【答案】(1)(ⅰ)見解析(ⅱ)沒有![]() 的把握認(rèn)為“物理考試成績是否達(dá)到級與性別有關(guān)”(2)見解析,
的把握認(rèn)為“物理考試成績是否達(dá)到級與性別有關(guān)”(2)見解析,![]()
【解析】
(1)完善列聯(lián)表,計算![]() ,得到答案.
,得到答案.
(2)![]() 的所有取值為0,1,2,3,且
的所有取值為0,1,2,3,且![]() ,計算概率得到分布列,計算數(shù)學(xué)期望得到答案.
,計算概率得到分布列,計算數(shù)學(xué)期望得到答案.
(1)(ⅰ)
考試成績達(dá)到 | 考試成績未達(dá)到 | 總計 | |
男生 | 14 | 26 | 40 |
女生 | 6 | 24 | 30 |
總計 | 20 | 50 | 70 |
(ⅱ)![]() ,
,
所以沒有![]() 的把握認(rèn)為“物理考試成績是否達(dá)到級與性別有關(guān)”.
的把握認(rèn)為“物理考試成績是否達(dá)到級與性別有關(guān)”.
(2)由(1)知從該校高三年級任意抽取1名學(xué)生的成績,物理考試成績達(dá)到![]() 級的概率
級的概率![]() ,
,![]() 的所有取值為0,1,2,3,且
的所有取值為0,1,2,3,且![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.


 優(yōu)化作業(yè)上海科技文獻(xiàn)出版社系列答案
優(yōu)化作業(yè)上海科技文獻(xiàn)出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 平行,求
平行,求![]() 的值及
的值及![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時,求證:
時,求證:![]() 在定義域內(nèi)有且只有兩個極值點.
在定義域內(nèi)有且只有兩個極值點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() 、
、![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,
,![]() ,
,![]() 為其右焦點,
為其右焦點,![]() ,且該橢圓的離心率為
,且該橢圓的離心率為![]() ;
;
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 軸上方的點
軸上方的點![]() ,交直線
,交直線![]() 于點
于點![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,直線
,直線![]() 與直線
與直線![]() 交于點
交于點![]() .若
.若![]() ,求
,求![]() 取值范圍.
取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
|
某商場經(jīng)銷某商品,根據(jù)以往資料統(tǒng)計,顧客采用的付款期數(shù)![]() 的分布列為
的分布列為
商場經(jīng)銷一件該商品,采用1期付款,其利潤為200元;分2期或3期付款,其利潤為250元;分4期或5期付款,其利潤為300元.![]() 表示經(jīng)銷一件該商品的利潤.
表示經(jīng)銷一件該商品的利潤.
(Ⅰ)求事件A:“購買該商品的3位顧客中,至少有1位采用1期付款”的概率
P(A);
(Ⅱ)求![]() 的分布列及期望
的分布列及期望![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年“兩會”報告指出,5G在下半年會零星推出,2020年有望實現(xiàn)大范圍使用。隨著移動通信產(chǎn)業(yè)的發(fā)展,全球移動寬帶(![]() ,簡稱
,簡稱![]() )用戶數(shù)已達(dá)54億,占比70%(
)用戶數(shù)已達(dá)54億,占比70%(![]() 用戶比例簡稱
用戶比例簡稱![]() 滲透率),但在部分發(fā)展中國家該比例甚至低于20%。
滲透率),但在部分發(fā)展中國家該比例甚至低于20%。
|
| 總計 | |
| |||
| |||
總計 |
(1)現(xiàn)對140個發(fā)展中國家進(jìn)行調(diào)查,發(fā)現(xiàn)140個發(fā)展中國家中有25個國家MBB基站覆蓋率小于80%,其中![]() 滲透率低于20%的有15個國家,而
滲透率低于20%的有15個國家,而![]() 基站覆蓋率大于80%的國家中
基站覆蓋率大于80%的國家中![]() 滲透率低于20%的有25個國家.由以上統(tǒng)計數(shù)據(jù)完成下面
滲透率低于20%的有25個國家.由以上統(tǒng)計數(shù)據(jù)完成下面![]() 列聯(lián)表,并判斷是否有99%的把握認(rèn)為
列聯(lián)表,并判斷是否有99%的把握認(rèn)為![]() 滲透率與
滲透率與![]() 基站覆蓋率有關(guān);
基站覆蓋率有關(guān);
(2)![]() 基站覆蓋率小于80%,其中
基站覆蓋率小于80%,其中![]() 滲透率低于20%的國家中
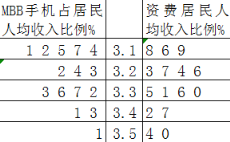
滲透率低于20%的國家中![]() 手機(jī)占居民人均收入比例和資費居民人均收入比例如莖葉圖所示,請根據(jù)莖葉圖求這些國家中的
手機(jī)占居民人均收入比例和資費居民人均收入比例如莖葉圖所示,請根據(jù)莖葉圖求這些國家中的![]() 手機(jī)占居民人均收入比例的中位數(shù)和資費居民人均收入比例平均數(shù);
手機(jī)占居民人均收入比例的中位數(shù)和資費居民人均收入比例平均數(shù);
(3)根據(jù)以上數(shù)據(jù)判斷,若要提升![]() 滲透率,消除數(shù)字化鴻溝,把數(shù)字世界帶入每個人,需要重點解決哪些問題。
滲透率,消除數(shù)字化鴻溝,把數(shù)字世界帶入每個人,需要重點解決哪些問題。
附:參考公式:![]() ;其中
;其中![]() .
.
臨界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某次知識競賽規(guī)則如下:在主辦方預(yù)設(shè)的5個問題中,選手若能連續(xù)正確回答出兩個問題,即停止答題,晉級下一輪。假設(shè)某選手正確回答每個問題的概率都是0.8,且每個問題的回答結(jié)果相互獨立,則該選手恰好回答了4個問題就晉級下一輪的概率等于( )。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是等差數(shù)列,其前
是等差數(shù)列,其前![]() 項中的奇數(shù)項的和與偶數(shù)項的和之差為
項中的奇數(shù)項的和與偶數(shù)項的和之差為![]() .
.
(1)請證明這一結(jié)論對任意等差數(shù)列![]() (
(![]() 中各項均不為零)恒成立;
中各項均不為零)恒成立;
(2)請類比等差數(shù)列的結(jié)論,對于各項均為正數(shù)的等比數(shù)列![]() ,提出猜想,并加以證明.
,提出猜想,并加以證明.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com