
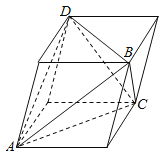
【題目】若四面體![]() 的三組對棱分別相等,即
的三組對棱分別相等,即![]() ,給出下列結論:
,給出下列結論:
①四面體![]() 每組對棱相互垂直;
每組對棱相互垂直;
②四面體![]() 每個面的面積相等;
每個面的面積相等;
③從四面體![]() 每個頂點出發的三條棱兩兩夾角之和大
每個頂點出發的三條棱兩兩夾角之和大![]() 而小于
而小于![]() ;
;
④連接四面體![]() 每組對棱中點的線段相互垂直平分.
每組對棱中點的線段相互垂直平分.
其中正確結論的序號是__________. (寫出所有正確結論的序號)
【答案】②④.
【解析】分析:①將四面體ABCD的三組對棱分別看作平行六面體的對角線,由于三組對棱分別相等,所以平行六面體為長方體.結合長方體的性質判斷
②四面體ABCD的每個面是全等的三角形,面積是相等的.
③由②,從四面體ABCD每個頂點出發的三條棱兩兩夾角能夠等量代換為同一個三角形內的三個內角,它們之和為180°.
④連接四面體ABCD每組對棱中點構成菱形,線段互垂直平分
詳解::①將四面體ABCD的三組對棱分別看作平行六面體的對角線,由于三組對棱分別相等,所以平行六面體為長方體.
由于長方體的各面不一定為正方形,所以同一面上的面對角線不一定垂直,從而每組對棱不一定相互垂直.①錯誤
②四面體ABCD的每個面是全等的三角形,面積是相等的.②正確
③由②,四面體ABCD的每個面是全等的三角形,從四面體ABCD每個頂點出發的三條棱兩兩夾角能夠等量代換為同一個三角形內的三個內角,它們之和為180°.③錯誤
④連接四面體ABCD每組對棱中點構成菱形,線段互垂直平分④正確
故答案為②④


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案科目:高中數學 來源: 題型:
【題目】已知冪函數f(x)=x![]() (m∈N*).
(m∈N*).
(1)試確定該函數的定義域,并指明該函數在其定義域上的單調性;
(2)若該函數還經過點(2, ![]() ),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數a的取值范圍.
),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠今年擬舉行促銷活動,經調查測算,該廠產品的年銷售量(即該廠的年產量)x(萬件)與年促銷費m(萬元)(m≥0)滿足x=3-![]() .已知今年生產的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金).
.已知今年生產的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金).
(1)將今年該產品的利潤y(萬元)表示為年促銷費m(萬元)的函數;
(2)求今年該產品利潤的最大值,此時促銷費為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位有員工1000名,平均每人每年創造利潤10萬元.為增加企業競爭力,決定優化產業結構,調整出![]() 名員工從事第三產業,調整后平均每人每年創造利潤為
名員工從事第三產業,調整后平均每人每年創造利潤為![]() 萬元
萬元![]() ,剩下的員工平均每人每年創造的利潤可以提高
,剩下的員工平均每人每年創造的利潤可以提高![]() .
.
(1)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多調整出多少名員工從事第三產業?
(2)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤條件下,若要求調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤,則![]() 的取值范圍是多少?
的取值范圍是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大型綜藝節目《最強大腦》中,有一個游戲叫做盲擰魔方,就是玩家先觀察魔方狀態并進行記憶,記住后蒙住眼睛快速還原魔方,盲擰在外人看來很神奇,其實原理是十分簡單的,要學會盲擰也是很容易的.根據調查顯示,是否喜歡盲擰魔方與性別有關.為了驗證這個結論,某興趣小組隨機抽取了50名魔方愛好者進行調查,其中喜歡盲擰的30人中男性22人,女性人數正好等于男性不喜歡盲擰人數.
(1)請完成下面的![]() 列聯表
列聯表
喜歡盲擰 | 不喜歡盲擰 | 總計 | |
男 | |||
女 | |||
總計 |
并判斷能否在犯錯誤的概率不超過0.025的前提下認為是否喜歡盲擰與性別有關?
(2)現邀請其中20名男生參加盲擰三階魔方比賽,其完成情況如下表所示.
成功完成時間(分鐘) |
|
|
|
|
人數 | 10 | 3 | 5 | 2 |
現從表中成功完成時間在![]() 和
和![]() 這兩組內的7名男生中任意抽取2人對他們的盲擰情況進行視頻記錄,求2人成功完成時間恰好在同一組內的概率.
這兩組內的7名男生中任意抽取2人對他們的盲擰情況進行視頻記錄,求2人成功完成時間恰好在同一組內的概率.
附參考公式及參考數據: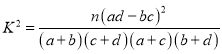 ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)選修4-4:坐標系與參數方程
在直角坐標系xOy中,曲線![]() 的參數方程為
的參數方程為![]() 為參數),M為
為參數),M為![]() 上的動點,P點滿足
上的動點,P點滿足![]() ,點P的軌跡為曲線
,點P的軌跡為曲線![]() .
.
(I)求![]() 的方程;
的方程;
(II)在以O為極點,x軸的正半軸為極軸的極坐標系中,射線![]() 與
與![]() 的異于極點的交點為A,與
的異于極點的交點為A,與![]() 的異于極點的交點為B,求|AB|.
的異于極點的交點為B,求|AB|.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com