【題目】如圖，四棱錐
，底面
是
的菱形，側(cè)面
是邊長為
的正三角形，O是AD的中點， 
為
的中點．
（1）求證：
；
（2）若PO與底面ABCD垂直，求直線
與平面
所成的角的正弦值．
【答案】（1）詳見解析（2）
【解析】
試題分析：（I）取AD中點 O，連接OP，OC，AC，證明OC⊥AD，OP⊥AD．推出AD⊥平面POC，即可在，PC⊥AD．（II）證明PO⊥平面ABCD．說明PO為三棱錐P-ACD的高．求出△PAC的面積，設點D到平面 PAC的距離為h，由VD-PAC=VP-ACD，求出點D到平面PAC的距離，然后求解直線DM與平面PAC所成的角的正弦值
試題解析：（1）連接
，
，
由題意可知
，
均為正三角形．
所以
，
．
又
，
平面
，
平面
，
所以
平面
，
又
平面
，
所以
．
（2）又
平面
．即
為三棱錐
的高．
在
中，
，
在
中，
，
，
邊
上的高
，
所以
的面積
．
設點
到平面
的距離為
，由
得，
，
又
，
所以
，解得
．
故點
到平面
的距離為
．
設直線
與平面所成的角為
則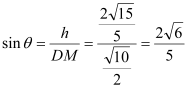
，
所以直線與平面所成的角的正弦值為．
科目：高中數(shù)學 來源： 題型：
【題目】如圖1，已知四邊形
為直角梯形， 
， 
， 
， 
為等邊三角形， 
， 
，如圖2，將
， 
分別沿
折起，使得平面
平面
，平面
平面
，連接
，設
為
上任意一點．
（1）證明： 
平面
；
（2）若
，求
的值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
（
為自然對數(shù)的底數(shù)）．
（1）求函數(shù)
的單調(diào)區(qū)間；
（2）設函數(shù)
，存在
，
，使得成立
成立，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為了比較兩種治療失眠癥的藥（分別稱為A藥,B藥）的療效,隨機地選取20位患者服用A藥,20位患者服用B藥,這40位患者在服用一段時間后,記錄他們?nèi)掌骄黾拥乃邥r間（單位:h）,試驗的觀測結(jié)果如下:
服用A藥的20位患者日平均增加的睡眠時間:
服用B藥的20位患者日平均增加的睡眠時間:
（Ⅰ）分別計算兩組數(shù)據(jù)的平均數(shù),從計算結(jié)果看,哪種藥的療效更好？
（Ⅱ）根據(jù)兩組數(shù)據(jù)完成下面莖葉圖,從莖葉圖看,哪種藥的療效更好？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】函數(shù)f（x）對一切實數(shù)x，y均有f（x＋y）－f（y）＝（x＋2y＋1）x成立，且f（1）＝0．
（1）求f（0）；
（2）求f（x）；
（3）當0<x<2時不等式f（x）>ax－5恒成立，求a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】甲、乙、丙、丁、戊五人排成一排，甲和乙都排在丙的同一側(cè)，排法種數(shù)為
A. 80 B. 72 C. 60 D. 40
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
