
已知函數(shù)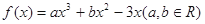 ,在點(diǎn)
,在點(diǎn)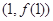 處的切線方程為
處的切線方程為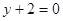 .
.
(Ⅰ)求函數(shù)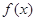 的解析式;
的解析式;
(Ⅱ)若對于區(qū)間 上任意兩個(gè)自變量的值
上任意兩個(gè)自變量的值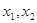 ,都有
,都有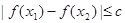 ,求實(shí)數(shù)
,求實(shí)數(shù)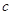 的最小值;
的最小值;
(Ⅲ)若過點(diǎn)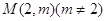 ,可作曲線
,可作曲線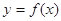 的三條切線,求實(shí)數(shù)
的三條切線,求實(shí)數(shù)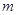 的取值范圍.
的取值范圍.
(1)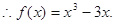
(2)4
(3)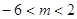
解析試題分析:(Ⅰ)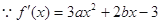
根據(jù)題意,得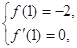 即
即
解得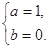
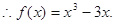
(Ⅱ)令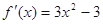
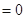 ,解得
,解得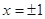
f(-1)=2, f(1)=-2,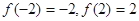
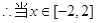 時(shí),
時(shí),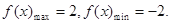
則對于區(qū)間[-2,2]上任意兩個(gè)自變量的值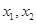 ,都有
,都有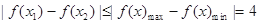
所以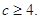 所以
所以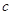 的最小值為4。
的最小值為4。
(Ⅲ)設(shè)切點(diǎn)為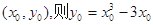
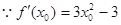 ,
, 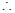 切線的斜率為
切線的斜率為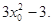
則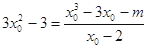
即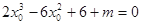 ,
,
因?yàn)檫^點(diǎn)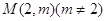 ,可作曲線
,可作曲線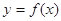 的三條切線
的三條切線
所以方程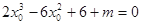 有三個(gè)不同的實(shí)數(shù)解
有三個(gè)不同的實(shí)數(shù)解
即函數(shù)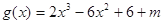 有三個(gè)不同的零點(diǎn),
有三個(gè)不同的零點(diǎn),
則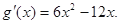
令