
【題目】平面直角坐標系中,動圓![]() 與圓
與圓![]() 外切,且與直線
外切,且與直線![]() 相切,記圓心
相切,記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)設過定點![]() (
(![]() 為非零常數)的動直線
為非零常數)的動直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,問:在曲線
兩點,問:在曲線![]() 上是否存在點
上是否存在點![]() (與
(與![]() 兩點相異),當直線
兩點相異),當直線![]() 的斜率存在時,直線
的斜率存在時,直線![]() 的斜率之和為定值.若存在,求出點
的斜率之和為定值.若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】【試題分析】(1)依據題設條件運用兩圓位置關系建立方程求解;(2)依據題設條件借助直線的斜率公式及直線與拋物線的位置關系進行分析求解:
(1)不妨設動圓![]() 的圓心為
的圓心為![]() ,
,
易知圓![]() 的圓心為
的圓心為![]() ,半徑為
,半徑為![]() ,
,
∵動圓![]() 與圓
與圓![]() 外切,且與直線
外切,且與直線![]() 相切,
相切,
∴圓心![]() 在直線
在直線![]() 的右側,且點
的右側,且點![]() 到點
到點![]() 的距離比點
的距離比點![]() 到直線
到直線![]() 的距離大
的距離大![]() ,
,
即![]() ,且
,且![]() ,
,
∴![]() ,兩邊平方并化簡整理得
,兩邊平方并化簡整理得![]() ,
,
即曲線![]() 的軌跡方程為
的軌跡方程為![]() .
.
(2)假設在曲線![]() 上存在點
上存在點![]() 滿足題設條件,不妨設
滿足題設條件,不妨設![]() ,
,
則![]() ,
,
∴![]() (*)
(*)
顯然動直線![]() 的斜率非零,故可設其方程為
的斜率非零,故可設其方程為![]() ,
,
聯立![]() ,整理得
,整理得![]() ,
,
∴![]() ,且
,且![]() ,
,
代入(*)式得![]() ,
,
顯然![]() ,于是
,于是![]() (**),
(**),
欲使(**)式對任意![]() 成立,∴
成立,∴ ,
,
顯然![]() ,否則由
,否則由![]() 可知
可知![]() ,
,
從而可得![]() ,這與
,這與![]() 為非零常數矛盾,
為非零常數矛盾,
∴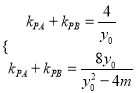 ,
,
∴![]() ,∴
,∴![]() ,
,
于是,當![]() 時,不存在滿足條件的
時,不存在滿足條件的![]() ,即不存在滿足題設條件的點
,即不存在滿足題設條件的點![]() ;
;
當![]() 時,
時, ![]() ,
,
將此代入拋物線![]() 的方程可求得滿足條件的
的方程可求得滿足條件的![]() 點坐標為
點坐標為![]() 或
或![]() .
.
下面說明此時直線![]() 的斜率必定存在,
的斜率必定存在,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
顯然![]() ,∴
,∴![]() ,且
,且![]() ,∴直線
,∴直線![]() 的斜率必定存在,
的斜率必定存在,
綜上所述,存在點![]() (與
(與![]() 兩點相異),其坐標為
兩點相異),其坐標為![]() ,或
,或![]() ,使得直線
,使得直線![]() 的斜率之和為定值.
的斜率之和為定值.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,
,![]() ,且對任意正整數n,點(
,且對任意正整數n,點(![]() ,
,![]() )在直線
)在直線![]() 上.
上.
(1)求數列![]() 的通項公式;
的通項公式;
(2)是否存在實數λ,使得數列{![]() }為等差數列?若存在,求出λ的值;若不存在,請說明理由;
}為等差數列?若存在,求出λ的值;若不存在,請說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.在(0, ![]() )內,sinx>cosx
)內,sinx>cosx
B.函數y=2sin(x+ ![]() )的圖象的一條對稱軸是x=
)的圖象的一條對稱軸是x= ![]() π
π
C.函數y= ![]() 的最大值為π
的最大值為π
D.函數y=sin2x的圖象可以由函數y=sin(2x﹣ ![]() )的圖象向右平移
)的圖象向右平移 ![]() 個單位得到
個單位得到
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數, ![]() ),以坐標原點為極點,
),以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系,圓
軸正半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)討論直線![]() 與圓
與圓![]() 的公共點個數;
的公共點個數;
(Ⅱ)過極點作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,求點
,求點![]() 的軌跡與圓
的軌跡與圓![]() 相交所得弦長.
相交所得弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據環境保護部《環境空氣質量指數(![]() )技術規定》,空氣質量指數(
)技術規定》,空氣質量指數(![]() )在201—300之間為重度污染;在301—500之間為嚴重污染.依據空氣質量預報,同時綜合考慮空氣污染程度和持續時間,將空氣重污染分4個預警級別,由輕到重依次為預警四級、預警三級、預警二級、預警一級,分別用藍、黃、橙、紅顏色標示,預警一級(紅色)為最高級別.(一)預警四級(藍色):預測未來1天出現重度污染;(二)預警三級(黃色):預測未來1天出現嚴重污染或持續3天出現重度污染;(三)預警二級(橙色);預測未來持續3天交替出現重度污染或嚴重污染;(四)預警一級(紅色);預測未來持續3天出現嚴重污染.
)在201—300之間為重度污染;在301—500之間為嚴重污染.依據空氣質量預報,同時綜合考慮空氣污染程度和持續時間,將空氣重污染分4個預警級別,由輕到重依次為預警四級、預警三級、預警二級、預警一級,分別用藍、黃、橙、紅顏色標示,預警一級(紅色)為最高級別.(一)預警四級(藍色):預測未來1天出現重度污染;(二)預警三級(黃色):預測未來1天出現嚴重污染或持續3天出現重度污染;(三)預警二級(橙色);預測未來持續3天交替出現重度污染或嚴重污染;(四)預警一級(紅色);預測未來持續3天出現嚴重污染.
某城市空氣質量監測部門對近300天空氣中![]() 濃度進行統計,得出這300天
濃度進行統計,得出這300天![]() 濃度的頻率分布直方圖如圖,將
濃度的頻率分布直方圖如圖,將![]() 濃度落入各組的頻率視為概率,并假設每天的
濃度落入各組的頻率視為概率,并假設每天的![]() 濃度相互獨立.
濃度相互獨立.
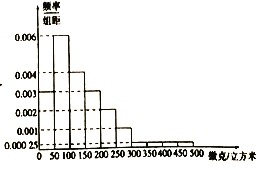
(1)求當地監測部門發布顏色預警的概率;
(2)據當地監測站數據顯示未來4天將出現3天嚴重污染,求監測部門發布紅色預警的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com