
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,
,![]() ,且對任意正整數n,點(
,且對任意正整數n,點(![]() ,
,![]() )在直線
)在直線![]() 上.
上.
(1)求數列![]() 的通項公式;
的通項公式;
(2)是否存在實數λ,使得數列{![]() }為等差數列?若存在,求出λ的值;若不存在,請說明理由;
}為等差數列?若存在,求出λ的值;若不存在,請說明理由;
【答案】(1)an=(![]() )n-1;(2)λ=2.
)n-1;(2)λ=2.
【解析】試題分析:(Ⅰ)利用數列{an}的前n項Sn與an的關系得到數列相鄰項之間的關系式,![]() 為等比數列,進而確定出其通項公式;
為等比數列,進而確定出其通項公式;
(Ⅱ)確定出數列{an}的前n項和為Sn的表達式是解決本題的關鍵,數列為等差數列首先保證其前3項滿足等差數列的關系,得出關于λ的方程,從而確定出λ的值.
試題解析:
(1)由2an+1+Sn-2=0①
當n≥2時2an+Sn-1-2=0② ∴2an+1-2an+an=0 ∴![]() =
=![]() (n≥2)
(n≥2)
∵a1=1,2a2+a1=2a2=![]() ∴{an}是首項為1,公比為
∴{an}是首項為1,公比為![]() 的等比數列,
的等比數列,
∴an=(![]() )n-1.
)n-1.
(2)Sn=2-![]()
若![]() 為等差數列,則S1+λ+
為等差數列,則S1+λ+![]() ,S2+2λ+
,S2+2λ+![]() ,S3+3λ+
,S3+3λ+![]() 成等差數列,∴2(S2+2λ+
成等差數列,∴2(S2+2λ+![]() )=S1+
)=S1+![]() λ+S3+
λ+S3+![]() ∴λ=2,經檢驗知
∴λ=2,經檢驗知![]() 為等差數列。
為等差數列。


科目:高中數學 來源: 題型:
【題目】如圖,將數字1,2,3,…, ![]() (
(![]() )全部填入一個2行
)全部填入一個2行![]() 列的表格中,每格填一個數字,第一行填入的數字依次為
列的表格中,每格填一個數字,第一行填入的數字依次為![]() ,
, ![]() ,…,
,…, ![]() ,第二行填入的數字依次為
,第二行填入的數字依次為![]() ,
, ![]() ,…,
,…, ![]() .記
.記![]() .
.

(Ⅰ)當![]() 時,若
時,若![]() ,
, ![]() ,
, ![]() ,寫出
,寫出![]() 的所有可能的取值;
的所有可能的取值;
(Ⅱ)給定正整數![]() .試給出
.試給出![]() ,
, ![]() ,…,
,…, ![]() 的一組取值,使得無論
的一組取值,使得無論![]() ,
, ![]() ,…,
,…, ![]() 填寫的順序如何,
填寫的順序如何, ![]() 都只有一個取值,并求出此時
都只有一個取值,并求出此時![]() 的值;
的值;
(Ⅲ)求證:對于給定的![]() 以及滿足條件的所有填法,
以及滿足條件的所有填法, ![]() 的所有取值的奇偶性相同.
的所有取值的奇偶性相同.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面給出了四個類比推理:
①![]() 為實數,若
為實數,若![]() 則
則![]() ;類比推出:
;類比推出: ![]() 為復數,若
為復數,若![]() 則
則![]() .
.
② 若數列![]() 是等差數列,
是等差數列, ![]() ,則數列
,則數列![]() 也是等差數列;類比推出:若數列
也是等差數列;類比推出:若數列![]() 是各項都為正數的等比數列,
是各項都為正數的等比數列, ![]() ,則數列
,則數列![]() 也是等比數列.
也是等比數列.
③ 若![]() 則
則![]() ; 類比推出:若
; 類比推出:若![]() 為三個向量,則
為三個向量,則![]() .
.
④ 若圓的半徑為![]() ,則圓的面積為
,則圓的面積為![]() ;類比推出:若橢圓的長半軸長為
;類比推出:若橢圓的長半軸長為![]() ,短半軸長為
,短半軸長為![]() ,則橢圓的面積為
,則橢圓的面積為![]() .上述四個推理中,結論正確的是( )
.上述四個推理中,結論正確的是( )
A. ① ② B. ② ③ C. ① ④ D. ② ④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點
的焦點![]() 在直線
在直線![]() 上,且拋物線
上,且拋物線![]() 截直線
截直線![]() 所得的弦
所得的弦![]() 的長為
的長為![]() .
.
(Ⅰ)求拋物線![]() 的方程和
的方程和![]() 的值.
的值.
(Ⅱ)以弦![]() 為底邊,以
為底邊,以![]() 軸上點
軸上點![]() 為頂點的三角形
為頂點的三角形![]() 面積為
面積為![]() ,求點
,求點![]() 坐標.
坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() ,過點
,過點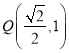 作圓
作圓![]() 的切線,切點分別為
的切線,切點分別為![]() ,
, ![]() ,直線
,直線![]() 恰好經過橢圓
恰好經過橢圓![]() 的右頂點和上頂點.
的右頂點和上頂點.
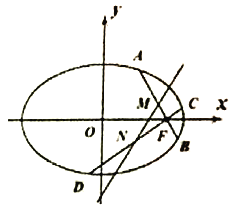
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)如圖,過橢圓![]() 的右焦點
的右焦點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() ,
, ![]() ,設
,設![]() ,
, ![]() 的中點分別為
的中點分別為![]() ,
, ![]() ,證明:直線
,證明:直線![]() 必過定點,并求此定點坐標.
必過定點,并求此定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的不等式ax2+5x+c>0的解集為{x| ![]() <x<
<x< ![]() },
},
(1)求a,c的值;
(2)解關于x的不等式ax2+(ac+b)x+bc≥0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系中,動圓![]() 與圓
與圓![]() 外切,且與直線
外切,且與直線![]() 相切,記圓心
相切,記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)設過定點![]() (
(![]() 為非零常數)的動直線
為非零常數)的動直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,問:在曲線
兩點,問:在曲線![]() 上是否存在點
上是否存在點![]() (與
(與![]() 兩點相異),當直線
兩點相異),當直線![]() 的斜率存在時,直線
的斜率存在時,直線![]() 的斜率之和為定值.若存在,求出點
的斜率之和為定值.若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com