
【題目】一青蛙從點![]() 開始依次水平向右和豎直向上跳動,其落點坐標依次是
開始依次水平向右和豎直向上跳動,其落點坐標依次是![]()
![]() ,(如圖所示,
,(如圖所示,![]() 坐標以已知條件為準),
坐標以已知條件為準),![]() 表示青蛙從點
表示青蛙從點![]() 到點
到點![]() 所經過的路程.
所經過的路程.

(1)若點![]() 為拋物線
為拋物線![]() (
(![]() )準線上一點,點
)準線上一點,點![]() 均在該拋物線上,并且直線
均在該拋物線上,并且直線![]() 經過該拋物線的焦點,證明
經過該拋物線的焦點,證明![]() .
.
(2)若點![]() 要么落在
要么落在![]() 所表示的曲線上,要么落在
所表示的曲線上,要么落在![]() 所表示的曲線上,并且
所表示的曲線上,并且![]() ,試寫出
,試寫出![]() (不需證明);
(不需證明);
(3)若點![]() 要么落在
要么落在![]() 所表示的曲線上,要么落在
所表示的曲線上,要么落在![]() 所表示的曲線上,并且
所表示的曲線上,并且![]() ,求
,求![]() 的表達式.
的表達式.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)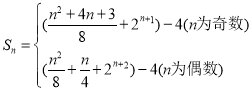 .
.
【解析】
試題分析:(1)直接借助題設求解即可獲證;(2)運用題設條件和極限思想表示出來再求解即可;(3)運用題設中提供的信息分類進行求解.
試題解析:(1)設![]() ,由于青蛙依次向右向上跳動,
,由于青蛙依次向右向上跳動,
所以![]() ,
,![]() ,由拋物線定義知:
,由拋物線定義知:![]() .
.
(2)依題意,![]() ,
,![]() ,
,![]() (
(![]() )
)
![]()
![]()
![]()
隨著![]() 的增大,點
的增大,點![]() 無限接近點
無限接近點![]() ,
,
橫向路程之和無限接近![]() ,縱向路程之和無限接近
,縱向路程之和無限接近![]() ,
,
所以![]() .
.
(3)方法一:設點![]() ,則題意,
,則題意,![]() 的坐標滿足如下遞推關系:
的坐標滿足如下遞推關系:
![]() ,且
,且![]() ,
,![]() (
(![]() )
)
其中![]() ,
,![]()
∴![]() ,即
,即![]() ,
,
∴![]() 是以
是以![]() 為首項,2為公差的等差數列,
為首項,2為公差的等差數列,
∴![]() ,
,
所以當![]() 為偶數時,
為偶數時,![]() ,于是
,于是![]() ,
,
又![]() ,
,
∴當![]() 為奇數時,
為奇數時,![]() ,
,![]() ,
,
當![]() 為偶數時,
為偶數時,
![]()
![]()
![]()
![]()
當![]() 為奇數時,
為奇數時,
![]()
![]()
![]()
![]()
所以,當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]()
所以,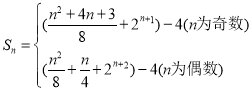 .
.
方法二:由題意知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…
其中![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…
![]() ,
,![]() ,
,![]() ,
,![]() …
…
觀察規律可知:下標為奇數的點的縱坐標為首項為![]() ,公比為4的等比數列,相鄰橫坐標之差為首項為2,公差為1的等差數列,下標為偶數的點也有此規律,并由數學歸納法可以證明.
,公比為4的等比數列,相鄰橫坐標之差為首項為2,公差為1的等差數列,下標為偶數的點也有此規律,并由數學歸納法可以證明.
所以,當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]() ,
,
當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]()
所以,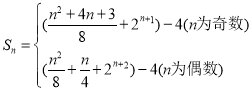 .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】網絡購物已經被大多數人接受,隨著時間的推移,網絡購物的人越來越多,然而也有部分人對網絡購物的質量和信譽產生懷疑。對此,某新聞媒體進行了調查,在所有參與調查的人中,持“支持”和“不支持”態度的人數如下表所示:
年齡 態度 | 支持 | 不支持 |
20歲以上50歲以下 | 800 | 200 |
50歲以 (含50歲) | 100 | 300 |
(1)在所有參與調查的人中,用分層抽樣的方法抽取![]() 個人,已知從持“支持”態度的人中抽取了9人,求
個人,已知從持“支持”態度的人中抽取了9人,求![]() 的值;
的值;
(2)是否有99.9%的把握認為支持網絡購物與年齡有關?
參考數據:
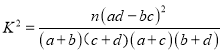 ,其中
,其中![]() ,
,
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某漁場魚群的最大養殖量為![]() 噸,為保證魚群的生長空間,實際的養殖量
噸,為保證魚群的生長空間,實際的養殖量![]() 要小于
要小于![]() ,留出適當的空閑量,空閑量與最大養殖量的比值叫空閑率,已知魚群的年增加量
,留出適當的空閑量,空閑量與最大養殖量的比值叫空閑率,已知魚群的年增加量![]() (噸)和實際養殖量
(噸)和實際養殖量![]() (噸)與空閑率的乘積成正比(設比例系數
(噸)與空閑率的乘積成正比(設比例系數![]() ).
).
(1)寫出![]() 與
與![]() 的函數關系式,并指出定義域;
的函數關系式,并指出定義域;
(2)求魚群年增長量的最大值;
(3)當魚群年增長量達到最大值時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某生態園將一三角形地塊![]() 的一角
的一角![]() 開辟為水果園種植桃樹,已知角
開辟為水果園種植桃樹,已知角![]() 為
為![]() ,
,![]() 的長度均大于
的長度均大于![]() 米,現在邊界
米,現在邊界![]() 處建圍墻,在
處建圍墻,在![]() 處圍竹籬笆.
處圍竹籬笆.
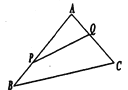
(1)若圍墻![]() 總 長度為
總 長度為![]() 米,如何圍可使得三角形地塊
米,如何圍可使得三角形地塊![]() 的面積最大?
的面積最大?
(2)已知![]() 段圍墻高
段圍墻高![]() 米,
米,![]() 段圍墻高
段圍墻高![]() 米,造價均為每平方米
米,造價均為每平方米![]() 元.若圍圍墻用了
元.若圍圍墻用了![]() 元,問如何圍可使竹籬笆用料最省?
元,問如何圍可使竹籬笆用料最省?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的是
A. 若直線![]() 與平面
與平面![]() 平行,則
平行,則![]() 與平面
與平面![]() 內的任意一條直線都沒有公共點;
內的任意一條直線都沒有公共點;
B. 若直線![]() 與平面
與平面![]() 平行,則
平行,則![]() 與平面
與平面![]() 內的任意一條直線都平行;
內的任意一條直線都平行;
C. 若直線![]() 上有無數個點不在平面
上有無數個點不在平面 ![]() 內,則
內,則![]() ;
;
D. 如果兩條平行線中的一條與一個平面平行,那么另一條也與這個平面平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() .
.
(1)若![]() 分別表示將一枚質地均勻的正方體骰子(六個面的點數分別為1,2,3,4,5,6)先后拋擲兩次時第一次、第二次出現的點數,求滿足
分別表示將一枚質地均勻的正方體骰子(六個面的點數分別為1,2,3,4,5,6)先后拋擲兩次時第一次、第二次出現的點數,求滿足![]() 的概率;
的概率;
(2)若![]() 在連續區間
在連續區間![]() 上取值,求滿足
上取值,求滿足![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com