
【題目】已知點![]() ,點
,點![]() 為曲線
為曲線![]() 上的動點,過
上的動點,過![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,滿足
,滿足![]() 。
。
(1)求曲線![]() 的方程;
的方程;
(2)直線![]() 與曲線
與曲線![]() 交于兩不同點
交于兩不同點![]() ,
,![]() ( 非原點),過
( 非原點),過![]() ,
,![]() 兩點分別作曲線
兩點分別作曲線![]() 的切線,兩切線的交點為
的切線,兩切線的交點為![]() 。設線段
。設線段![]() 的中點為
的中點為![]() ,若
,若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
【題目】近年來,我國工業經濟發展迅速,工業增加值連年攀升,某研究機構統計了近十年(從2008年到2017年)的工業增加值(萬億元),如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工業增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依據表格數據,得到下面的散點圖及一些統計量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
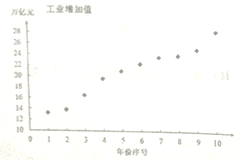
(1)根據散點圖和表中數據,此研究機構對工業增加值![]() (萬億元)與年份序號
(萬億元)與年份序號![]() 的回歸方程類型進行了擬合實驗,研究人員甲采用函數
的回歸方程類型進行了擬合實驗,研究人員甲采用函數![]() ,其擬合指數
,其擬合指數![]() ;研究人員乙采用函數
;研究人員乙采用函數![]() ,其擬合指數
,其擬合指數![]() ;研究人員丙采用線性函數
;研究人員丙采用線性函數![]() ,請計算其擬合指數,并用數據說明哪位研究人員的函數類型擬合效果最好.(注:相關系數
,請計算其擬合指數,并用數據說明哪位研究人員的函數類型擬合效果最好.(注:相關系數![]() 與擬合指數
與擬合指數![]() 滿足關系
滿足關系![]() ).
).
(2)根據(1)的判斷結果及統計值,建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01);
的回歸方程(系數精確到0.01);
(3)預測到哪一年的工業增加值能突破30萬億元大關.
附:樣本
![]() 的相關系數
的相關系數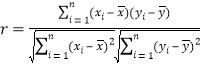 ,
,
![]() ,
,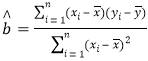 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 分別為
分別為![]() 的左、右頂點,
的左、右頂點,![]() 是
是![]() 上異于
上異于![]() 的動點,
的動點,![]() 面積的最大值為2.
面積的最大值為2.
(1)求橢圓![]() 的方程;
的方程;
(2)證明:直線![]() 與直線
與直線![]() 的斜率乘積為定值;
的斜率乘積為定值;
(3)設直線![]() ,
,![]() 分別交直線
分別交直線![]() 于
于![]() 兩點,以
兩點,以![]() 為直徑作圓,當圓的面積最小時,求該圓的方程.
為直徑作圓,當圓的面積最小時,求該圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“難度系數”反映試題的難易程度,難度系數越大,題目得分率越高,難度也就越小.“難度系數”的計算公式為![]() ,其中,
,其中,![]() 為難度系數,
為難度系數,![]() 為樣本平均失分,
為樣本平均失分,![]() 為試卷總分(一般為100分或150分).某校高三年級的李老師命制了某專題共5套測試卷(每套總分150分),用于對該校高三年級480名學生進行每周測試.測試前根據自己對學生的了解,預估了每套試卷的難度系數,如下表所示:
為試卷總分(一般為100分或150分).某校高三年級的李老師命制了某專題共5套測試卷(每套總分150分),用于對該校高三年級480名學生進行每周測試.測試前根據自己對學生的了解,預估了每套試卷的難度系數,如下表所示:
試卷序號 | 1 | 2 | 3 | 4 | 5 |
考前預估難度系數 | 0.7 | 0.64 | 0.6 | 0.6 | 0.55 |
測試后,隨機抽取了50名學生的數據進行統計,結果如下:
試卷序號 | 1 | 2 | 3 | 4 | 5 |
實測平均分 | 102 | 99 | 93 | 93 | 87 |
(1)根據試卷2的難度系數估計這480名學生第2套試卷的平均分;
(2)從抽樣的50名學生的5套試卷中隨機抽取2套試卷,記這2套試卷中平均分超過96分的套數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)試卷的預估難度系數和實測難度系數之間會有偏差.設![]() 為第
為第![]() 套試卷的實測難度系數,并定義統計量
套試卷的實測難度系數,并定義統計量![]() ,若
,若![]() ,則認為本專題的5套試卷測試的難度系數預估合理,否則認為不合理.試檢驗本專題的5套試卷對難度系數的預估是否合理.
,則認為本專題的5套試卷測試的難度系數預估合理,否則認為不合理.試檢驗本專題的5套試卷對難度系數的預估是否合理.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級的全體學生平均分成![]() 個小組,且每個小組均有
個小組,且每個小組均有![]() 名男生和多名女生.現從各個小組中隨機抽取一名同學參加社區服務活動,若抽取的
名男生和多名女生.現從各個小組中隨機抽取一名同學參加社區服務活動,若抽取的![]() 名學生中至少有一名男生的概率為
名學生中至少有一名男生的概率為![]() ,則( )
,則( )
A.該班級共有![]() 名學生
名學生
B.第一小組的男生甲被抽去參加社區服務的概率為![]()
C.抽取的![]() 名學生中男女生數量相同的概率是
名學生中男女生數量相同的概率是![]()
D.設抽取的![]() 名學生中女生數量為
名學生中女生數量為![]() ,則
,則![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() ,橢圓
,橢圓![]() 分別為橢圓的左、右焦點.
分別為橢圓的左、右焦點.
(1)當直線![]() 過右焦點
過右焦點![]() 時,求橢圓
時,求橢圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,
兩點,![]() 為坐標原點,且
為坐標原點,且![]() ,若點
,若點![]() 在以線段
在以線段![]() 為直徑的圓內,求實數
為直徑的圓內,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com