
【題目】已知函數f(x)=x2ex﹣b,其中b∈R.
(Ⅰ)證明:對于任意x1,x2∈(﹣∞,0],都有f(x1)﹣f(x2)![]() ;
;
(Ⅱ)討論函數f(x)的零點個數(結論不需要證明).
【答案】(Ⅰ)詳見解析;(Ⅱ)詳見解析.
【解析】
(I)利用導數求得函數的最大值和最小值,利用最大值減去最小值來證得不等式成立.(II)當![]() 和
和![]() 時,由
時,由![]() 解析式判斷零點的個數.當
解析式判斷零點的個數.當![]() 時,根據最大值進行分類,得出零點個數.
時,根據最大值進行分類,得出零點個數.
解:(Ⅰ)f(x)的定義域R,且f′(x)=x(x+2)ex,
令f′(x)=0則x1=0,或x2=﹣2,
f′(x)=x(x+2)ex,
x | (﹣∞,﹣2) | ﹣2 | (﹣2,0) |
f′(x) | + | 0 | ﹣ |
f(x) | 增函數 | 極大值 | 減函數 |
∴f(x)在區間(﹣∞,0]上的最大值為;f(﹣2)![]() b,
b,
∵x∈(﹣∞,0],∴f(x)=x2ex﹣b≥﹣b,
∴f(x)的最小值為:﹣b,
∴對于任意x1,x2∈(﹣∞,0],都有f(x1)﹣f(x2)≤f(x)最大值﹣f(x)![]() ;
;
(Ⅱ)f′(x)=x(x+2)ex,函數f(x)=x2ex﹣b,
當b<0時,函數f(x)=x2ex﹣b>0恒成立,函數f(x)的零點個數為:0
當b=0時,函數f(x)=x2ex,函數f(x)的零點個數為:1
當b![]() 時,函數f(x)的零點個數為;2,
時,函數f(x)的零點個數為;2,
當0<b![]() 時,函數f(x)的零點個數為:3,
時,函數f(x)的零點個數為:3,
當b![]() 時,函數f(x)的零點個數為:1,
時,函數f(x)的零點個數為:1,


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() ,曲線
,曲線![]() 為參數), 以坐標原點
為參數), 以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)若射線![]() 分別交
分別交![]() 于
于![]() 兩點, 求
兩點, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 漢字聽寫大會
漢字聽寫大會![]() 不斷創收視新高,為了避免“書寫危機”,弘揚傳統文化,某市大約10萬名市民進行了漢字聽寫測試
不斷創收視新高,為了避免“書寫危機”,弘揚傳統文化,某市大約10萬名市民進行了漢字聽寫測試![]() 現從某社區居民中隨機抽取50名市民的聽寫測試情況,發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第1組
現從某社區居民中隨機抽取50名市民的聽寫測試情況,發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第1組![]() ,第2組
,第2組![]() ,
,![]() ,第6組
,第6組![]() ,如圖是按上述分組方法得到的頻率分布直方圖.
,如圖是按上述分組方法得到的頻率分布直方圖.

![]() 若電視臺記者要從抽取的市民中選1人進行采訪,求被采訪人恰好在第2組或第6組的概率;
若電視臺記者要從抽取的市民中選1人進行采訪,求被采訪人恰好在第2組或第6組的概率;
![]() 試估計該市市民正確書寫漢字的個數的平均數與中位數;
試估計該市市民正確書寫漢字的個數的平均數與中位數;
![]() 已知第4組市民中有3名男性,組織方要從第4組中隨機抽取2名市民組成弘揚傳統文化宣傳隊,求至少有1名女性市民的概率.
已知第4組市民中有3名男性,組織方要從第4組中隨機抽取2名市民組成弘揚傳統文化宣傳隊,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有關于![]() 的一元二次方程
的一元二次方程![]() .
.
(Ⅰ)若![]() 是從
是從![]() 四個數中任取的一個數,
四個數中任取的一個數,![]() 是從
是從![]() 三個數中任取的一個數,求上述方程有實根的概率.
三個數中任取的一個數,求上述方程有實根的概率.
(Ⅱ)若![]() 是從區間
是從區間![]() 任取的一個數,
任取的一個數,![]() 是從區間
是從區間![]() 任取的一個數,求上述方程有實根的概率.
任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() ∶
∶![]() 和圓
和圓![]() ∶
∶![]() ,
,![]() 是直線
是直線![]() 上一點,過點
上一點,過點![]() 作圓
作圓![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() .
.
(1)若![]() ,求點
,求點![]() 坐標;
坐標;
(2)若圓![]() 上存在點
上存在點![]() ,使得
,使得![]() ,求點
,求點![]() 的橫坐標的取值范圍;
的橫坐標的取值范圍;
(3)設線段![]() 的中點為
的中點為![]() ,
,![]() 與
與![]() 軸的交點為
軸的交點為![]() ,求線段
,求線段![]() 長的最大值.
長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
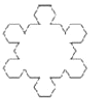
【題目】如圖,第1個圖形由正三角形擴展而成,共12個頂點.第n個圖形是由正n+2邊形擴展而來 ![]() ,則第n+1個圖形的頂點個數是 ( )
,則第n+1個圖形的頂點個數是 ( )
 (1)
(1)  (2)
(2) (3)
(3)  (4)
(4)
A. (2n+1)(2n+2)B. 3(2n+2)C. (n+2)(n+3)D. (n+3)(n+4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的有______個.
①空間中三條直線交于一點,則這三條直線共面;
②一個平行四邊形確定一個平面;
③若一個角的兩邊分別平行于另一個角的兩邊,則這兩個角相等;
④已知兩個不同的平面![]() 和
和![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,則點
,則點![]() 在直線
在直線![]() 上.
上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com