
【題目】已知函數(shù)f(x)= ![]() .
.
(I)討論函數(shù)的單調性,并證明當x>﹣2時,xex+2+x+4>0;
(Ⅱ)證明:當a∈[0,1)時,函數(shù)g(x)= ![]() (x>﹣2)有最小值,設g(x)最小值為h(a),求函數(shù)h(a)的值域.
(x>﹣2)有最小值,設g(x)最小值為h(a),求函數(shù)h(a)的值域.
【答案】解:(Ⅰ)證明:由 ![]() ,
,
得 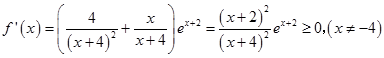 ,
,
故f(x)在(﹣∞,﹣4)和(﹣4,+∞)上單調遞增,
當x>﹣2時,由上知f(x)>f(﹣2)=﹣1,
即 ![]() ,即xex+2+x+4>0,得證.
,即xex+2+x+4>0,得證.
(Ⅱ)對 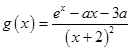 求導,
求導,
得 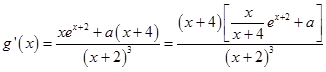 ,x>﹣2.
,x>﹣2.
記 ![]() ,x>﹣2.
,x>﹣2.
由(Ⅰ)知,函數(shù)φ(x)區(qū)間(﹣2,+∞)內單調遞增,
又φ(﹣2)=﹣1+a<0,φ(0)=a>0,所以存在唯一正實數(shù)x0,使得 ![]() .
.
于是,當x∈(﹣2,x0)時,φ(x)<0,g'(x)<0,
函數(shù)g(x)在區(qū)間(﹣2,x0)內單調遞減;
當x∈(x0,+∞)時,φ(x)>0,g'(x)>0,
函數(shù)g(x)在區(qū)間(x0,+∞)內單調遞增.
所以g(x)在(﹣2,+∞)內有最小值 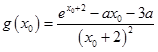 ,
,
由題設即 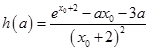 .
.
又因為 ![]() .所以
.所以 ![]() .
.
根據(jù)(Ⅰ)知,f(x)在(﹣2,+∞)內單調遞增,
![]() ,所以﹣2<x0≤0.
,所以﹣2<x0≤0.
令 ![]() ,
,
則 ![]() ,函數(shù)u(x)在區(qū)間(﹣2,0]內單調遞增,
,函數(shù)u(x)在區(qū)間(﹣2,0]內單調遞增,
所以u(﹣2)<u(x)≤u(0),
即函數(shù)h(a)的值域為 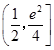
【解析】(Ⅰ)求出函數(shù)的導數(shù),解關于導函數(shù)的不等式,求出函數(shù)的單調區(qū)間,得到f(x)>f(﹣2),證明結論即可;(Ⅱ)求出g(x)的導數(shù),得到g(x)的最小值,分離a,得到 ![]() ,所以﹣2<x0≤0.令
,所以﹣2<x0≤0.令 ![]() ,根據(jù)函數(shù)的單調性判斷即可.
,根據(jù)函數(shù)的單調性判斷即可.
【考點精析】掌握利用導數(shù)研究函數(shù)的單調性是解答本題的根本,需要知道一般的,函數(shù)的單調性與其導數(shù)的正負有如下關系: 在某個區(qū)間![]() 內,(1)如果
內,(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調遞增;(2)如果
在這個區(qū)間單調遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調遞減.
在這個區(qū)間單調遞減.


科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)f(x)=(x2﹣ax+a+1)ex(a∈N)在區(qū)間(1,3)只有1個極值點,則曲線f(x)在點(0,f(0))處切線的方程為 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2011年,國際數(shù)學協(xié)會正式宣布,將每年的3月14日設為國際數(shù)學節(jié),來源則是中國古代數(shù)學家祖沖之的圓周率.祖沖之,在世界數(shù)學史上第一次將圓周率(π)值計算到小數(shù)點后的第7位,即3.1415926到3.1415927之間,數(shù)列{an}是公差大于0的等差數(shù)列,其前三項是“31415926”中連續(xù)的三個數(shù),數(shù)列{bn}是等比數(shù)列,其公比大于1的正整數(shù)且前三項是“31415926”中的三個數(shù),且a3=b3 .
(Ⅰ)求數(shù)列{an},{bn}的通項公式;
(Ⅱ)cn= 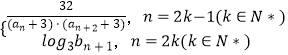 ,求c1+c2+c3+…+c
,求c1+c2+c3+…+c ![]() .(n∈N*)
.(n∈N*)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓E: ![]() +
+ ![]() =1(a>b>0)過點
=1(a>b>0)過點 ![]() ,且離心率e為
,且離心率e為 ![]() .
. 
(1)求橢圓E的方程;
(2)設直線x=my﹣1(m∈R)交橢圓E于A,B兩點,判斷點G ![]() 與以線段AB為直徑的圓的位置關系,并說明理由.
與以線段AB為直徑的圓的位置關系,并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=lnx﹣x2與g(x)=(x﹣2)2﹣ ![]() ﹣m的圖象上存在關于(1,0)對稱的點,則實數(shù)m的取值范圍是( )
﹣m的圖象上存在關于(1,0)對稱的點,則實數(shù)m的取值范圍是( )
A.(﹣∞,1﹣ln2)
B.(﹣∞,1﹣ln2]
C.(1﹣ln2,+∞)
D.[1﹣ln2,+∞)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題中正確命題的個數(shù)是( ) ①對于命題p:x∈R,使得x2+x+1<0,則¬p:x∈R,均有x2+x+1>0;
②命題“已知x,y∈R,若x+y≠3,則x≠2或y≠1”是真命題;
③回歸直線的斜率的估計值為1.23,樣本點的中心為(4,5),則回歸直線方程為 ![]() =1.23x+0.08;
=1.23x+0.08;
④m=3是直線(m+3)x+my﹣2=0與直線mx﹣6y+5=0互相垂直的充要條件.
A.1
B.3
C.2
D.4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在某次試驗中,有兩個試驗數(shù)據(jù)![]() ,統(tǒng)計的結果如下面的表格1.
,統(tǒng)計的結果如下面的表格1.
(1)在給出的坐標系中畫出![]() 的散點圖; 并判斷正負相關;
的散點圖; 并判斷正負相關;
(2)填寫表格2,然后根據(jù)表格2的內容和公式求出![]() 對
對![]() 的回歸直線方程
的回歸直線方程![]() ,并估計當
,并估計當![]() 為10時
為10時![]() 的值是多少?(公式:
的值是多少?(公式: ,
,![]() )
)
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 4 | 5 |
表1

表格2
序號 | | | | |
1 | 1 | 2 | ||
2 | 2 | 3 | ||
3 | 3 | 4 | ||
4 | 4 | 4 | ||
5 | 5 | 5 | ||
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在極坐標系中,曲線C:ρ=2acosθ(a>0),l:ρcos(θ﹣ ![]() )=
)= ![]() ,C與l有且僅有一個公共點.
,C與l有且僅有一個公共點.
(Ⅰ)求a;
(Ⅱ)O為極點,A,B為C上的兩點,且∠AOB= ![]() ,求|OA|+|OB|的最大值.
,求|OA|+|OB|的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知雙曲線C:![]() 的兩個頂點分別為A,B,點P是C上異于A,B的一點,直線PA,PB的傾斜角分別為α,β.若
的兩個頂點分別為A,B,點P是C上異于A,B的一點,直線PA,PB的傾斜角分別為α,β.若![]() ,則C的離心率為( )
,則C的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com