
【題目】已知數列{an}的前n項和為Sn , 且a2=8,Sn= ![]() ﹣n﹣1.
﹣n﹣1.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)求數列{ ![]() }的前n項和Tn .
}的前n項和Tn .
【答案】解:(I)∵a2=8,Sn= ![]() ﹣n﹣1. ∴n≥2時,an=Sn﹣Sn﹣1=
﹣n﹣1. ∴n≥2時,an=Sn﹣Sn﹣1= ![]() ﹣n﹣1﹣
﹣n﹣1﹣ ![]() ,化為:an+1=3an+2,
,化為:an+1=3an+2,
∴an+1+1=3(an+1),∴數列{an+1}是等比數列,第二項為9,公比為3.
∴an+1=9×3n﹣2=3n .
∴an=3n﹣1.
(II) ![]() =
=  =
= ![]() ﹣
﹣ ![]() .
.
∴數列{ ![]() }的前n項和Tn=
}的前n項和Tn= ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() ﹣
﹣ ![]()
【解析】(I)由a2=8,Sn= ![]() ﹣n﹣1.可得n≥2時,an=Sn﹣Sn﹣1 , 化為:an+1+1=3(an+1),利用等比數列的通項公式可得an . (II)
﹣n﹣1.可得n≥2時,an=Sn﹣Sn﹣1 , 化為:an+1+1=3(an+1),利用等比數列的通項公式可得an . (II) ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() .利用“裂項求和”方法即可得出.
.利用“裂項求和”方法即可得出.
【考點精析】掌握數列的前n項和和數列的通項公式是解答本題的根本,需要知道數列{an}的前n項和sn與通項an的關系 ;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為 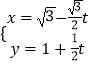 (t為參數),以坐標原點O為極點,以x軸正半軸為極軸,建立極坐標系,圓C的極坐標方程為
(t為參數),以坐標原點O為極點,以x軸正半軸為極軸,建立極坐標系,圓C的極坐標方程為 ![]() .
.
(1)求圓C的直角坐標方程;
(2)若P(x,y)是直線l與圓面 ![]() 的公共點,求
的公共點,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在底面是直角梯形的四棱錐S-ABCD中,![]() 面
面![]() .
.

(1)求四棱錐S-ABCD的體積;
(2)求證:面![]()
![]()
(3)求SC與底面ABCD所成角的正切值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四面體![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
,
![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證: ![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)求四面體![]() 的外接球的表面積.
的外接球的表面積.
(注:如果一個多面體的頂點都在球面上,那么常把該球稱為多面體的外接球. 球的表面積![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設小明訂了一份報紙,送報人可能在早上6:30﹣7:30之間把報紙送到,小明離家的時間在早上7:00﹣8:00之間,則他在離開家之前能拿到報紙的概率( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分13分)在四棱錐![]() 中,
中, ![]() ,
, ![]()
![]() ,
, ![]() 平面
平面![]() ,直線PC與平面ABCD所成角為
,直線PC與平面ABCD所成角為![]() ,
, ![]() .
.

(Ⅰ)求四棱錐![]() 的體積
的體積![]() ;
;
(Ⅱ)若![]() 為
為![]() 的中點,求證:平面
的中點,求證:平面![]()
![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的方程為
的方程為![]() ,直線
,直線![]() 的方程為
的方程為![]() ,點
,點![]() 在直線
在直線![]() 上,過點
上,過點![]() 作圓
作圓![]() 的切線
的切線![]() ,切點為
,切點為![]() .
.
(1)若點![]() 的坐標為
的坐標為![]() ,求切線
,求切線![]() 的方程;
的方程;
(2)求四邊形![]() 面積的最小值;
面積的最小值;
(3)求證:經過![]() 三點的圓必過定點,并求出所有定點坐標.
三點的圓必過定點,并求出所有定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若將函數y=2sin 2x的圖像向左平移 ![]() 個單位長度,則評議后圖象的對稱軸為( )
個單位長度,則評議后圖象的對稱軸為( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com