
【題目】當(dāng)|a|≤1,|x|≤1時(shí),關(guān)于x的不等式|x2﹣ax﹣a2|≤m恒成立,則實(shí)數(shù)m的取值范圍是( )
A.[ ![]() ,+∞)
,+∞)
B.[ ![]() ,+∞)
,+∞)
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,+∞)
,+∞)
【答案】B
【解析】解:|x2﹣ax﹣a2|=|﹣x2+ax+a2|≤|﹣x2+ax|+|a2|=|﹣x2+ax|+a2 , 當(dāng)且僅當(dāng)﹣x2+ax與a2同號(hào)時(shí)取等號(hào),
故當(dāng)﹣x2+ax≥0,有|x2﹣ax﹣a2|=﹣ ![]() +
+ ![]() a2 ,
a2 ,
當(dāng)x= ![]() 時(shí),取到最大值
時(shí),取到最大值 ![]() a2 , 而|a|≤1,|x|≤1,
a2 , 而|a|≤1,|x|≤1,
∴當(dāng)a=1,x= ![]() 或a=﹣1,x=﹣
或a=﹣1,x=﹣ ![]() 時(shí),
時(shí),
|x2﹣ax﹣a2|有最大值 ![]() ,
,
故m≥ ![]() ,
,
故選:B.
【考點(diǎn)精析】掌握絕對(duì)值不等式的解法是解答本題的根本,需要知道含絕對(duì)值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規(guī)律:關(guān)鍵是去掉絕對(duì)值的符號(hào).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ax2﹣2ax+1+b(a>0)在區(qū)間[2,3]上有最大值4和最小值1.
(Ⅰ)求實(shí)數(shù)a,b的值;
(Ⅱ)設(shè)函數(shù)g(x)=![]() ,若不等式g(2x)﹣k2x≤0在x∈[﹣1,1]上恒成立,求實(shí)數(shù)k的取值范圍.
,若不等式g(2x)﹣k2x≤0在x∈[﹣1,1]上恒成立,求實(shí)數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x+ ![]() +lnx,a∈R. (Ⅰ)若f(x)在x=1處取得極值,求a的值;
+lnx,a∈R. (Ⅰ)若f(x)在x=1處取得極值,求a的值;
(Ⅱ)若f(x)在區(qū)間(1,2)上單調(diào)遞增,求a的取值范圍;
(Ⅲ)討論函數(shù)g(x)=f'(x)﹣x的零點(diǎn)個(gè)數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l1:ax-by-1=0(a、b不同時(shí)為0),l2:(a+2)x+y+a=0.
(1)若b=0且l1⊥l2,求實(shí)數(shù)a的值;
(2)當(dāng)b=2,且l1∥l2時(shí),求直線l1與l2之間的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將三顆骰子各擲一次,記事件A=“三個(gè)點(diǎn)數(shù)都不同”,B=“至少出現(xiàn)一個(gè)6點(diǎn)”,則條件概率P(A|B),P(B|A)分別是( )
A.![]() ,
, ![]()
B.![]() ,
, ![]()
C.![]() ,
, ![]()
D.![]() ,
, ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知指數(shù)函數(shù)y=g(x)滿足:g(3)=8,定義域?yàn)镽的函數(shù)f(x)= ![]() 是奇函數(shù).
是奇函數(shù).
(1)確定y=g(x),y=f(x)的解析式;
(2)若h(x)=f(x)+a在(﹣1,1)上有零點(diǎn),求a的取值范圍;
(3)若對(duì)任意的t∈(﹣4,4),不等式f(6t﹣3)+f(t2﹣k)<0恒成立,求實(shí)數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點(diǎn),
的中點(diǎn), ![]() 是等腰三角形,
是等腰三角形, ![]() 是
是![]() 的中點(diǎn),
的中點(diǎn), ![]() 是
是![]() 上一點(diǎn).
上一點(diǎn).
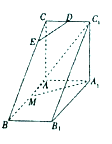
(Ⅰ)若![]() ,證明:
,證明: ![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△AOB中, ![]() ,斜邊AB=4,D是AB中點(diǎn),現(xiàn)將Rt△AOB以直角邊AO為軸旋轉(zhuǎn)一周得到一個(gè)圓錐,點(diǎn)C為圓錐底面圓周上一點(diǎn),且∠BOC=90°,
,斜邊AB=4,D是AB中點(diǎn),現(xiàn)將Rt△AOB以直角邊AO為軸旋轉(zhuǎn)一周得到一個(gè)圓錐,點(diǎn)C為圓錐底面圓周上一點(diǎn),且∠BOC=90°, 
(1)求圓錐的側(cè)面積;
(2)求直線CD與平面BOC所成的角的大小;(用反三角函數(shù)表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]() ,對(duì)任意
,對(duì)任意![]() 都有
都有![]() ,且當(dāng)
,且當(dāng)![]() 時(shí),
時(shí), ![]() .
.
(1)試判斷![]() 的單調(diào)性,并證明;
的單調(diào)性,并證明;
(2)若![]() ,
,
①求![]() 的值;
的值;
②求實(shí)數(shù)![]() 的取值范圍,使得方程
的取值范圍,使得方程![]() 有負(fù)實(shí)數(shù)根.
有負(fù)實(shí)數(shù)根.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com