
【題目】一士兵要在一個半徑為![]() 的圓形區域內檢查是否埋有地雷,他所用的檢查儀器的有效作用范圍的半徑為
的圓形區域內檢查是否埋有地雷,他所用的檢查儀器的有效作用范圍的半徑為![]() .求該士兵從該圓邊界上一點
.求該士兵從該圓邊界上一點![]() 出發,至少需走多少米才能將區域檢測完,且回到出發點?
出發,至少需走多少米才能將區域檢測完,且回到出發點?
【答案】![]()
【解析】
首先,求士兵從![]() 出發,將圓
出發,將圓![]() 的邊界上的所有點檢測完回到
的邊界上的所有點檢測完回到![]() 的最短路徑
的最短路徑![]() .
.
下面用反證法證明:
(1)![]() 上任意兩點連線段在
上任意兩點連線段在![]() 所圍區域內(含邊界),即
所圍區域內(含邊界),即![]() 是凸的;
是凸的;
(2)![]() 與圓
與圓![]() 內部無交點.
內部無交點.
(1)否則,設![]() 、
、![]() ,且線段
,且線段![]() 在
在![]() 所圍區域外(如圖).
所圍區域外(如圖).
用線段![]() 代替
代替![]() 中
中![]() 、
、![]() 間的曲線,得到另一條封閉曲線
間的曲線,得到另一條封閉曲線![]() .
.
則曲線![]() 在
在![]() 所圍區域內(含邊界).
所圍區域內(含邊界).
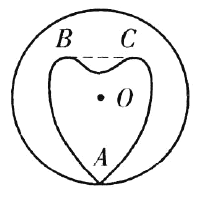
對圓![]() 邊界上任一點
邊界上任一點![]() ,設士兵在
,設士兵在![]() 上的點
上的點![]() 處檢測
處檢測![]() ,則
,則![]() .
.
取線段![]() 與
與![]() 的交點為
的交點為![]() ,則
,則![]() .
.
故士兵沿![]() 也可以將圓
也可以將圓![]() 的邊界上所有點檢測.
的邊界上所有點檢測.
但![]() 的長度小于
的長度小于![]() 的長度,矛盾.
的長度,矛盾.
(2)否則,設![]() 、
、![]() ,
,![]() 中
中![]() 、
、![]() 之間的曲線
之間的曲線![]() 在圓
在圓![]() 內部(如圖).
內部(如圖).
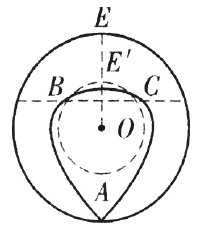
過圓心![]() 作
作![]() 交圓
交圓![]() 于點
于點![]() ,其中,
,其中,![]() 與曲線
與曲線![]() 在直線
在直線![]() 同側.
同側.
設線段![]() 與圓
與圓![]() 交于點
交于點![]() .
.
由![]() 的凸性知,曲線
的凸性知,曲線![]() 與
與![]() 的其余部分在直線
的其余部分在直線![]() 兩側.
兩側.
則![]() ,
,
即士兵沿![]() 無法檢測點
無法檢測點![]() ,矛盾.
,矛盾.
由(1),(2)知![]() 是含點
是含點![]() 且將圓
且將圓![]() 包含在內部的封閉曲線.
包含在內部的封閉曲線.
則![]() 的長度的最小值為
的長度的最小值為![]() (將
(將![]() 想成套在圓
想成套在圓![]() 上的繩子,當從點
上的繩子,當從點![]() 拉緊繩子時,得到繩子的最短長度為
拉緊繩子時,得到繩子的最短長度為![]() ).
).
易證當![]() 時,士兵可沿
時,士兵可沿![]() 將圓
將圓![]() 內所有點檢測.
內所有點檢測.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比數列,橢圓
成等比數列,橢圓![]() 上的點到焦點
上的點到焦點![]() 的距離的最大值為
的距離的最大值為![]() .
.
![]() 求橢圓
求橢圓![]() 的標準方程;
的標準方程;
![]() 過該橢圓的右焦點作兩條互相垂直的弦
過該橢圓的右焦點作兩條互相垂直的弦![]() 與
與![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某校5個學生的數學和物理成績如下:
學生的編號 | 1 | 2 | 3 | 4 | 5 |
數學成績 | 80 | 75 | 70 | 65 | 60 |
物理成績 | 70 | 66 | 68 | 64 | 62 |
(1)通過大量事實證明發現,一個學生的數學成績和物理成績是具有很強的線性相關關系的,在上述表格中,用![]() 表示數學成績,用
表示數學成績,用![]() 表示物理成績,求
表示物理成績,求![]() 關于
關于![]() 的回歸方程.
的回歸方程.
(2)利用殘差分析回歸方程的擬合效果,若殘差和在![]() 范圍內,則稱回歸方程為“優擬方程”,問:該回歸方程是否為“優擬方程”.
范圍內,則稱回歸方程為“優擬方程”,問:該回歸方程是否為“優擬方程”.
(3)現從5名同學中任選兩人參加訪談活動,求1號同學沒被選中的概率.
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: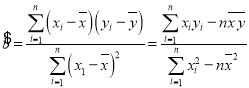 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 與
與![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 的交于
的交于![]() 點,
點,![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com