
【題目】已知函數{an}:a1=t,n2Sn+1=n2(Sn+an)+an2 , n=1,2,….
(1)設{an}為等差數列,且前兩項和S2=3,求t的值;
(2)若t= ![]() ,證明:
,證明: ![]() ≤an<1.
≤an<1.
【答案】
(1)解:設等差數列公差為d,則2t+d=3,
又 ![]() ,
,
得a1=1或a1=﹣3,
但當a1=﹣3時,d=9,無法使 ![]() 恒成立,
恒成立,
∴t=1.
(2)解:先證an<1.
易知an>0, ![]() ,故{an}為遞增數列,
,故{an}為遞增數列,
從而 ![]() ,
,
∴ ![]() 有
有 ![]() ,
,
由疊加法有 ![]() (n≥2),
(n≥2),
注意到 ![]() (k≥2),
(k≥2),
∴ ![]() ,
, ![]() =
= ![]()
從而 ![]() ,即an<1(n≥2),
,即an<1(n≥2),
又 ![]() ,有an<1(n∈N*)成立.
,有an<1(n∈N*)成立.
再證 ![]() ,
,
當n=1時, ![]() 成立,
成立,
由an<1, ![]() ,
,
從而 ![]()
![]() =
= ![]()
∴ ![]() ,即有
,即有 ![]() ,
,
疊加有 ![]() (n≥2),
(n≥2),
又 ![]() ,
,
從而 ![]()
![]() =
= ![]()
∴ ![]() ,即有
,即有 ![]() (n≥2),
(n≥2),
綜上 ![]() (n∈N*).
(n∈N*).
【解析】(1)利用等差數列的通項公式即可得出;(2)先證an<1.易知an>0,且{an}為遞增數列,利用遞推關系可得: ![]() ,利用“累加求和”方法即可證明.再證
,利用“累加求和”方法即可證明.再證 ![]() ,當n=1時,
,當n=1時, ![]() 成立,由an<1,可得:
成立,由an<1,可得: ![]() ,利用“累加求和”方法即可得出.
,利用“累加求和”方法即可得出.
【考點精析】認真審題,首先需要了解等差數列的通項公式(及其變式)(通項公式:![]() 或
或![]() ),還要掌握數列的通項公式(如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式)的相關知識才是答題的關鍵.
),還要掌握數列的通項公式(如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式)的相關知識才是答題的關鍵.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)已知遞增等差數列![]() 中的
中的![]() 是函數
是函數![]() 的兩個零點.數列
的兩個零點.數列![]() 滿足,點
滿足,點![]() 在直線
在直線![]() 上,其中
上,其中![]() 是數列
是數列![]() 的前
的前![]() 項和.
項和.
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)令![]() ,求數列
,求數列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知半徑為5的圓的圓心在![]() 軸上,圓心的橫坐標是整數,且與直線
軸上,圓心的橫坐標是整數,且與直線![]() 相切.
相切.
(1)求圓的方程;
(2)設直線![]() 與圓相交于
與圓相交于![]() 、
、![]() 兩點,求實數
兩點,求實數![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,是否存在實數![]() ,使得弦
,使得弦![]() 的垂直平分線
的垂直平分線![]() 過點
過點![]() ?若存在,求出實數
?若存在,求出實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】本著健康、低碳的生活理念,租自行車騎游的人越來越多.某自行車租車點的收費標準是每車每次租時間不超過兩小時免費,超過兩個小時的部分每小時收費2元(不足1小時的部分按1小時計算).有甲、乙兩人獨立來該租車點騎游(各組一車一次).設甲、乙不超過兩小時還車的概率分別為![]() ,
, ![]() ;兩小時以上且不超過三小時還車的概率分別為
;兩小時以上且不超過三小時還車的概率分別為![]() ,
, ![]() ;兩人租車時間都不會超過四小時.
;兩人租車時間都不會超過四小時.
(1)求甲、乙兩人所付租車費用相同的概率;
(2)設甲、乙兩人所付的租車費用之和為隨機變量![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直角三角形ABC中角A,B,C對邊長分別為a,b,c,∠C=90°.
(1)若三角形面積為2,求斜邊長c最小值;
(2)試比較an+bn與cn(n∈N*)的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高三年級從甲、乙兩個班級各選出7名學生參加數學競賽,他們取得的成績(滿分100分)的莖葉圖如圖,其中甲班學生成績的平均分是85,乙班學生成績的中位數是89.
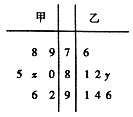
(1)求![]() 和
和![]() 的值;
的值;
(2)計算乙班7位學生成績的方差![]() .
.
(3)從成績在90分以上的學生中隨機抽取兩名學生,求乙班至少有一名學生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是等腰三角形,
是等腰三角形,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 上一點.
上一點.
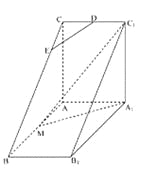
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 將三棱柱
將三棱柱![]() 分成兩個部分,求較小部分與較大部分的體積之比.
分成兩個部分,求較小部分與較大部分的體積之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C所對的邊分別為a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面積為3,求b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com