
【題目】某學校舉行了一次安全教育知識競賽,競賽的原始成績采用百分制.已知高三學生的原始成績均分布在![]() 內,發布成績使用等級制,各等級劃分標準見表.
內,發布成績使用等級制,各等級劃分標準見表.
原始成績 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等級 | 優秀 | 良好 | 及格 | 不及格 |
為了解該校高三年級學生安全教育學習情況,從中抽取了![]() 名學生的原始成績作為樣本進行統計,按照
名學生的原始成績作為樣本進行統計,按照![]() 的分組作出頻率分布直方圖如圖所示,其中等級為不及格的有5人,優秀的有3人.
的分組作出頻率分布直方圖如圖所示,其中等級為不及格的有5人,優秀的有3人.
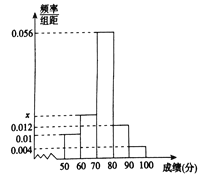
(1)求![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(2)根據樣本估計總體的思想,以事件發生的頻率作為相應事件發生的概率,若在該校高三學生中任選3人,求至少有1人成績是及格以上等級的概率;
(3)在選取的樣本中,從原始成績在80分以上的學生中隨機抽取3名學生進行學習經驗介紹,記![]() 表示抽取的3名學生中優秀等級的學生人數,求隨機變量
表示抽取的3名學生中優秀等級的學生人數,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案見解析.
;(3)答案見解析.
【解析】試題分析:
(1) 由題意可知,樣本容量![]() ,由頻率分布直方圖中小長方形面積之和為1可得
,由頻率分布直方圖中小長方形面積之和為1可得![]() .
.
(2)由題意可知,不及格的概率為0.1,由對立事件概率公式可得至少有1人成績是及格以上等級的概率為![]() ;
;
(3)由題意可知原始成績在80分以上的學生有![]() 人,優秀等級的學生有3人,則
人,優秀等級的學生有3人,則![]() 的取值可為0,1,2,3;計算相應的概率值可得
的取值可為0,1,2,3;計算相應的概率值可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,據此列出分布列,計算可得
,據此列出分布列,計算可得![]() 的數學期望為
的數學期望為![]() .
.
試題解析:
(1)由題意可知,樣本容量![]() ,
,
![]() ,
,
∴![]() .
.
(2)不及格的概率為0.1,設至少有1人成績是及格以上等級為事件![]() ,∴
,∴![]() ,故至少有1人成績是及格以上等級的概率為
,故至少有1人成績是及格以上等級的概率為![]() ;
;
(3)原始成績在80分以上的學生有![]() 人,優秀等級的學生有3人,
人,優秀等級的學生有3人,
∴![]() 的取值可為0,1,2,3;
的取值可為0,1,2,3;
∴![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
∴![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.


 優加精卷系列答案
優加精卷系列答案科目:高中數學 來源: 題型:
【題目】已知奇函數![]() (實數
(實數![]() 、
、![]() 為常數),且滿足
為常數),且滿足![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)試判斷函數![]() 在區間
在區間![]() 上的單調性,并用函數單調性定義證明;
上的單調性,并用函數單調性定義證明;
(3)當![]() 時,函數
時,函數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】先后拋擲兩枚骰子,設出現的點數之和是12,11,10的概率依次是P1,P2,P3,則( )
(A)P1=P2<P3 (B)P1<P2<P3 (C)P1<P2=P3 (D)P3=P2<P1
查看答案和解析>>
科目:高中數學 來源: 題型:
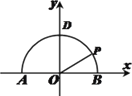
【題目】如圖![]() 為半圓
為半圓![]() 的直徑,點
的直徑,點![]() 是半圓弧上的兩點,
是半圓弧上的兩點, ![]() ,
, ![]() .曲線
.曲線![]() 經過點
經過點![]() ,且曲線
,且曲線![]() 上任意點
上任意點![]() 滿足:
滿足: ![]() 為定值.
為定值.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)設過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 面積最大時的直線
面積最大時的直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 是棱長為2的正方體
是棱長為2的正方體![]() 的棱
的棱![]() 的中點,點
的中點,點![]() 在面
在面![]() 所在的平面內,若平面
所在的平面內,若平面![]() 分別與平面
分別與平面![]() 和平面
和平面![]() 所成的銳二面角相等,則點
所成的銳二面角相等,則點![]() 到點
到點![]() 的最短距離是( )
的最短距離是( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品生產廠家根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品![]() (百臺),其總成本為
(百臺),其總成本為![]() (萬元),其中固定成本為
(萬元),其中固定成本為![]() 萬元,并且每生產
萬元,并且每生產![]() 百臺的生產成本為
百臺的生產成本為![]() 萬元(總成本
萬元(總成本![]() 固定成本
固定成本![]() 生產成本).銷售收入
生產成本).銷售收入![]() (萬元)滿足
(萬元)滿足![]() ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
(1)寫出利潤函數![]() 的解析式(利潤
的解析式(利潤![]() 銷售收入
銷售收入![]() 總成本);
總成本);
(2)工廠生產多少臺產品時,可使盈利最多?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com